– categories: 解题报告 comments: true title: “[NOIP2007]树网的核” layout: post tags:
- 图论
- 树
- 树的直径
- 数据结构
- 单调队列
-
two-pointers
题意
给出一棵树，求一条路径使得树上点到它的距离的最大值最小。
$n \leq 300000$.
思路
好题。
很早就看到过这个题目了，除了暴力没有任何思路……
今天学习了一下题解，发现还是很巧妙的。
Vmurder的题解
树的直径的性质
树的直径有什么性质呢？回顾一下两次 DFS 找树的直径的过程，我们可以得到以下的性质：
1. 树上的任何一个点的最远点，一定是某条直径的端点。
2. 所有直径中点过定点。
分析
我们可以证明，最优选定路径一定在某条直径上。 （如果证明有问题欢迎留言= =） 这需要分2种情况讨论。我们采用反证法。
- 选定的路径与直径不相交。这时我们需要证明选定路径不是最优的。如图，$<a, b>$ 为直径，$<c,d>$ 为选定路径。我们发现，如果 $c$ 左侧有点 $c’$, $d$ 右侧有点 $d’$, 那么一定有 $\vert fc’ \vert < \vert af \vert$ ；对 $d$ 而言也有 $\vert fd’ \vert < \vert fb \vert$，也就是说把选定路径长度不变地移动到直径 $ab$ 上，且盖住 $f$，答案只会更好。
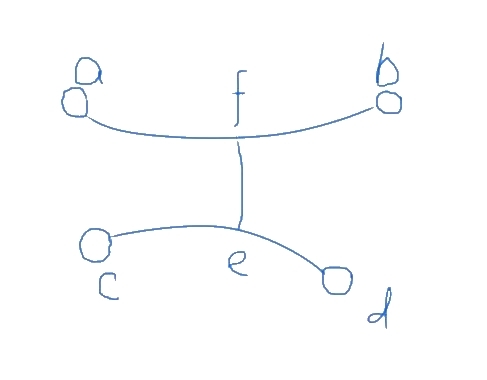
- 路径与直径有部分重合（自然也包含全部重合的情况）。如图。
在这种情况下，由直径的性质可知 $\vert be \vert \ge \vert de \vert$, 于是把 $\vert ed \vert$ 一段移动到 $\vert eb \vert$，答案不会更差。
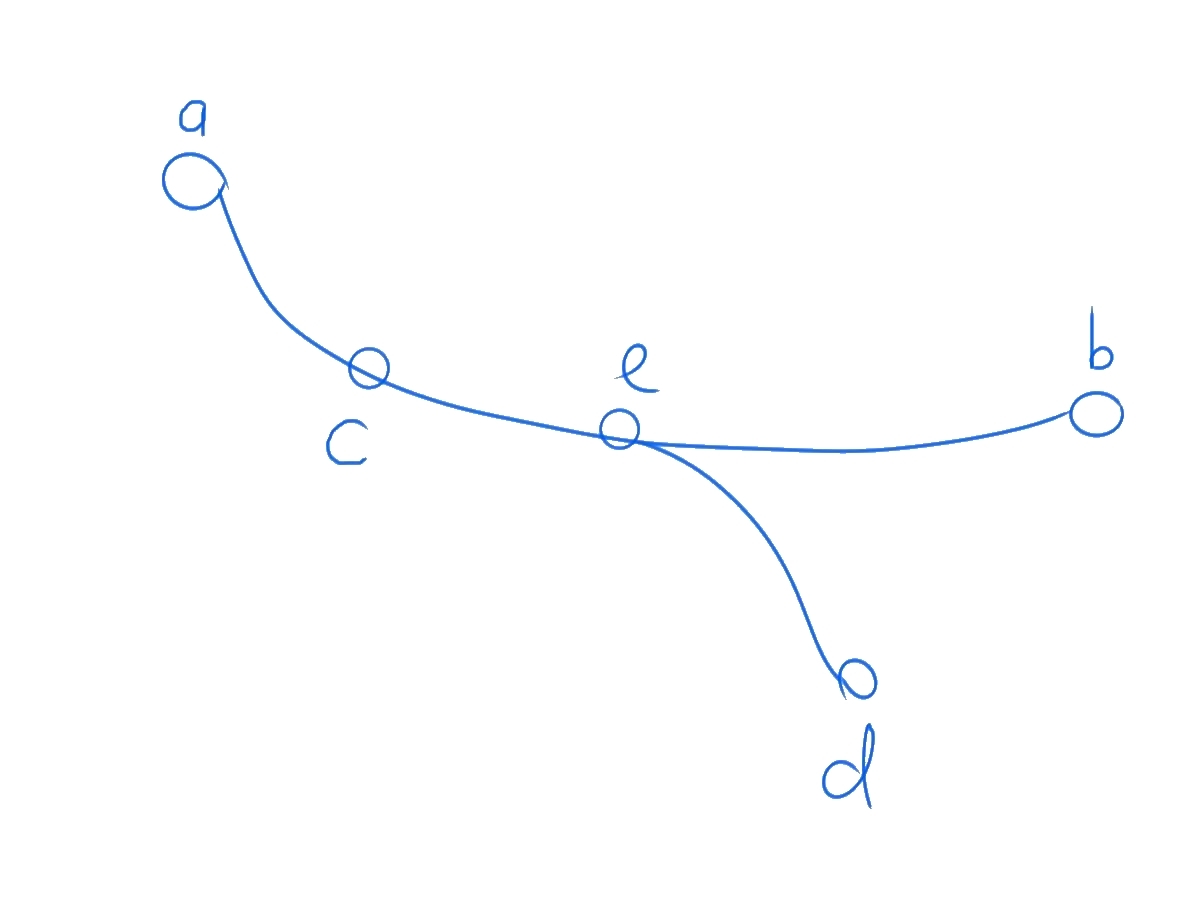于是命题得证。
我们再证明，即使存在多条直径，最优解也满足上述性质。
不失一般性，我们分析2条直径，且树的中心在边上的情况。
于是一定有 $\vert ap \vert = \vert a’p \vert, \vert bq \vert = \vert b’q \vert$. 不妨称之为性质3. 显然，由于$\vert pa’ \vert \le \vert pb \vert, \vert qb’ \vert \le \vert qa \vert$ ，红色和黄色的路径都不会是最优解。而对于绿色路径，由于直径的性质3，取在哪条直径都一样。于是得证。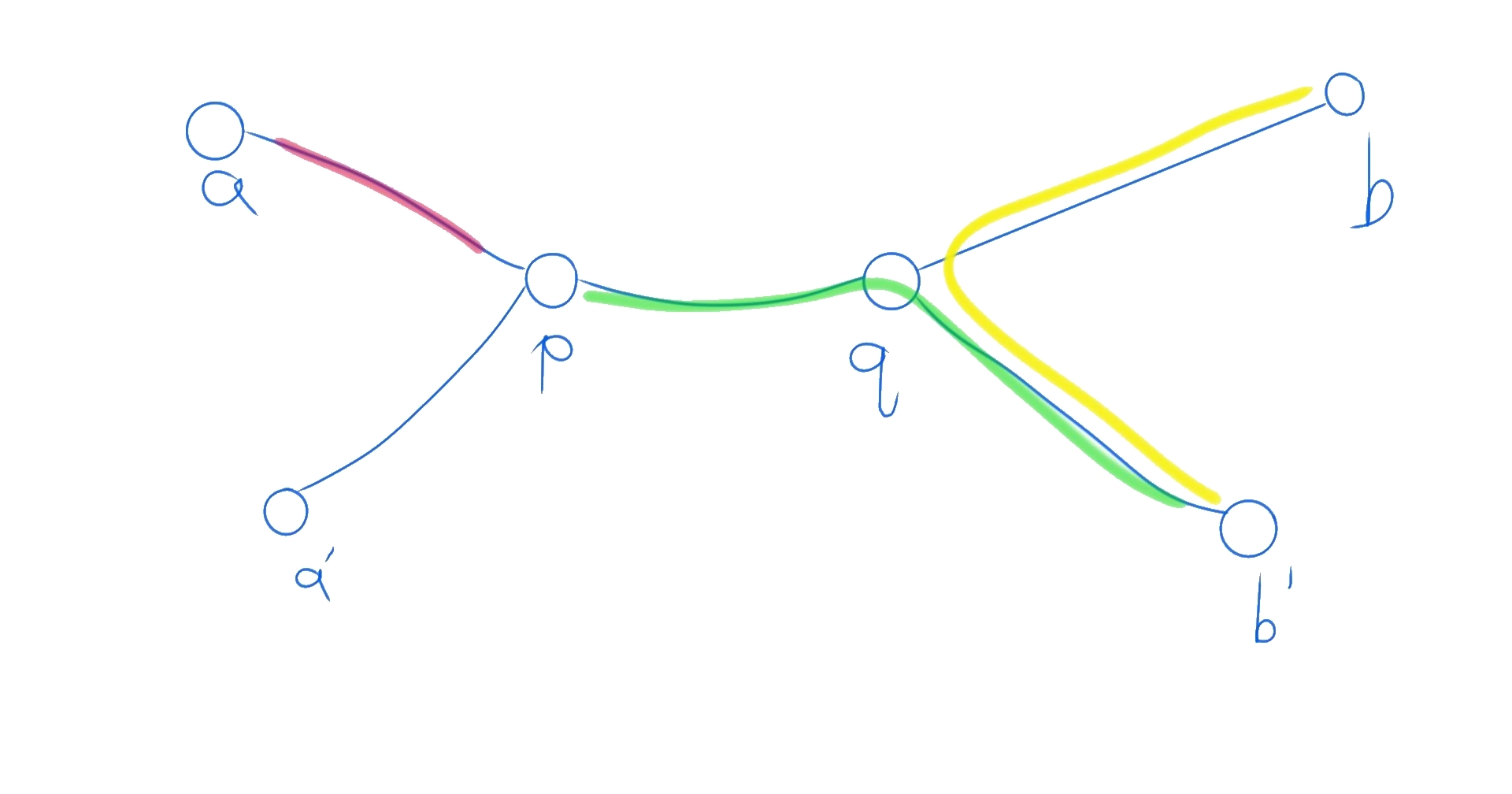
———————————-
证明了上述的定理，我们就可以设计主算法了：
- 2次BFS找出直径。这对于带有任意非负权值的树都成立！！！
- 显然贪心地取得最大可行长度的路径，答案不会更差。于是用 two-pointers 从直径的一端向另一端扫。如图。引用chrt学姐的一句话：
换一种看待树的方式，把直径横着，其他点挂在下方。（就像架子上的葡萄～）
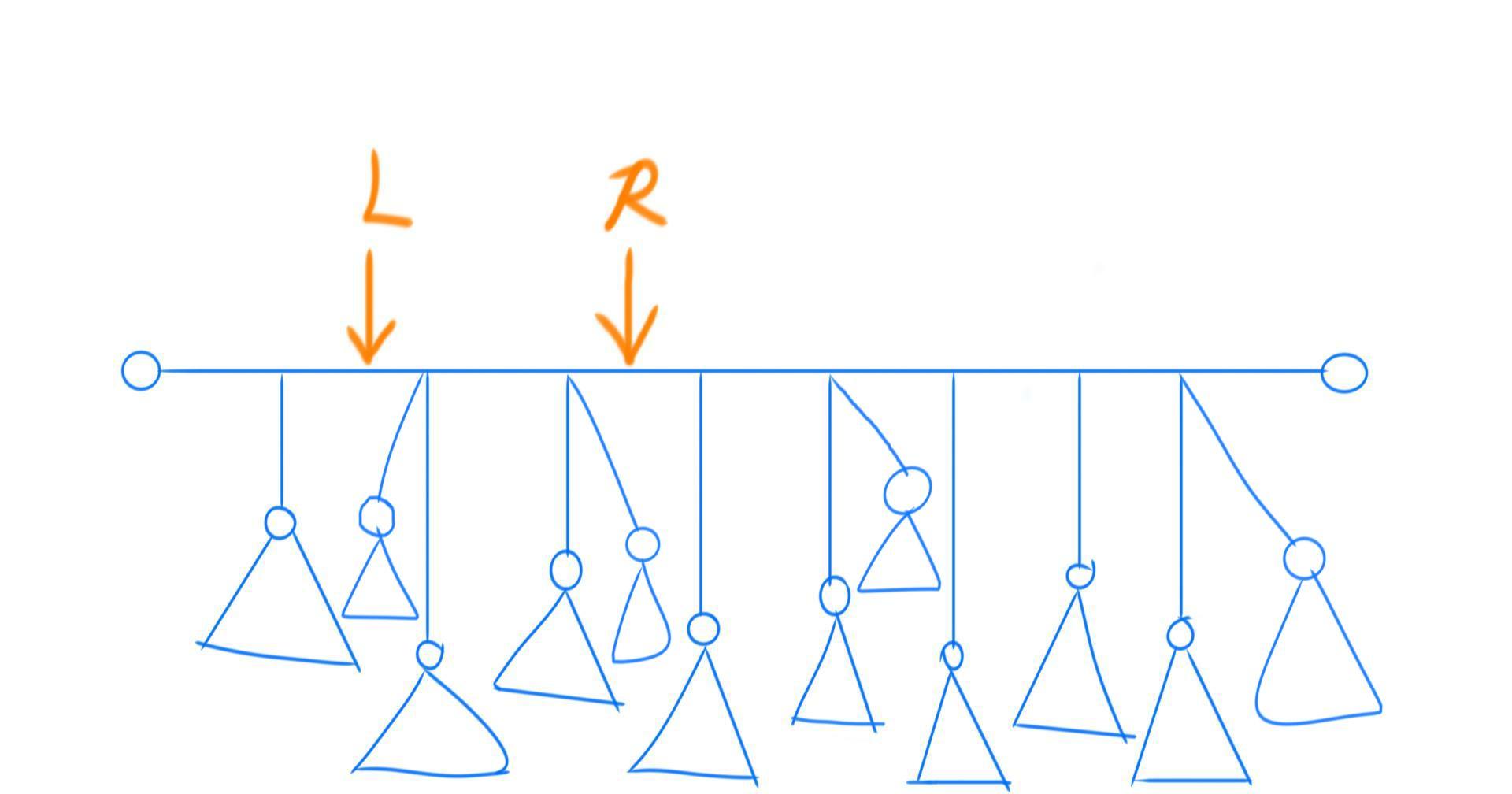然后每次在满足长度限制的条件下尽量扩展 R 指针，每次扩展到不能再扩展之后，用L左侧的最大距离、R右侧的最大距离， $[L, R]$ 区间内最大距离更新答案。前两者可以线性递推，第三个类似滑动窗口，直接用单调队列更新即可。
一点吐槽
- 一定要记住，两次BFS找出直径，对于带有任意非负权值的树都成立……今年的冬令营第一题的44分送分里面就用了这个。我以为这个只对于无权的树成立，然后不知道怎么办。忽然想起来前几天看的点分治，然而根本没写过，当场yy怎么写……然后T2的送50分就没调出来……出考场之后，cxy神犇跟我说，我才发现……囧rz
- 第一次看到这个加强版是在chrt的某个NOIP模拟赛里面……这个题目其实就是[SDOI2011]消防……那场模拟赛第一题是[SDOI2010]地精部落……emmmmmm，难度略高于某些年份的NOIP。
代码
#include <bits/stdc++.h>
#define max3(x, y, z) max((x), max((y), (z)))
using namespace std;
const int MAXN = 1e6, INF = 0x3f3f3f3f;
struct Edge {
int u, v, len, next;
};
int N, S, A, B, e_ptr = 1, head[MAXN+10]; Edge E[(MAXN+10)<<1];
int d[MAXN+10], p[MAXN+10]; bool vis[MAXN+10], Diameter[MAXN+10];
int Hd = 1, Tl = 0, Maxv[MAXN+10], MaxL[MAXN+10], MaxR[MAXN+10], MQ[MAXN+10];
vector<int> vec;
void AddEdge(int u, int v, int len) {
E[++e_ptr] = (Edge) { u, v, len, head[u] }; head[u] = e_ptr;
}
void AddPair(int u, int v, int len) {
AddEdge(u, v, len); AddEdge(v, u, len);
}
void BFS(int st) {
queue<int> Q;
memset(d, -1, sizeof(d));
memset(p, 0, sizeof(p));
Q.push(st); d[st] = 0;
while(!Q.empty()) {
int u = Q.front(); Q.pop();
for(int j=head[u]; j; j=E[j].next) {
int v = E[j].v, len = E[j].len;
if(d[v] != -1) continue;
p[v] = j, d[v] = d[u] + len;
Q.push(v);
}
}
}
void DFS(int u) {
vis[u] = true;
for(int j=head[u]; j; j=E[j].next) {
int v = E[j].v, len = E[j].len;
if(vis[v] || Diameter[v])
continue;
DFS(v);
Maxv[u] = max(Maxv[u], Maxv[v] + len);
}
}
inline int readint() {
int f=1, r=0; char c=getchar();
while(!isdigit(c)) { if(c=='-')f=-1; c=getchar(); }
while(isdigit(c)) { r=r*10+c-'0'; c=getchar(); }
return f*r;
}
void Init() {
int u, v, w, MaxP, MaxV;
N = readint(); S = readint();
for(int i = 1; i <= N-1; i++) {
u = readint(); v = readint(); w = readint();
AddPair(u, v, w);
}
BFS(1); MaxP = MaxV = 0;
for(int i = 1; i <= N; i++)
if(MaxV < d[i]) {
MaxV = d[i];
MaxP = i;
}
B = MaxP;
BFS(B); MaxP = MaxV = 0;
for(int i = 1; i <= N; i++)
if(MaxV < d[i]) {
MaxV = d[i];
MaxP = i;
}
A = MaxP;
}
void PushMQ(int pos) {
while(Hd <= Tl && Maxv[vec[ MQ[Tl] ]] <= Maxv[vec[pos]])
--Tl;
MQ[++Tl] = pos;
}
void PopMQ(int pos) {
if(MQ[Hd] > pos) return;
assert(MQ[Hd] == pos);
++Hd;
}
void Work() {
int L, R, Len, Ans = INF; L = R = Len = 0;
for(int u = A; u != B; u = E[p[u]].u) {
Diameter[u] = true; vec.push_back(u);
}
Diameter[B] = true; vec.push_back(B);
// Init Maxv
for(int t = 0; t <= vec.size()-1; t++) {
int u = vec[t];
for(int j=head[u]; j; j=E[j].next) {
int v = E[j].v, len = E[j].len;
if(Diameter[v]) continue;
DFS(v); Maxv[u] = max(Maxv[u], Maxv[v] + len);
}
}
// Init MaxL
MaxL[A] = 0;
for(int t = 1; t <= vec.size()-1; t++) {
int u = vec[t];
MaxL[u] = max(MaxL[vec[t-1]], Maxv[vec[t-1]]) + E[p[ vec[t-1] ]].len;
}
// Init MaxR
MaxR[B] = 0;
for(int t = vec.size()-2; t >= 0; t--) {
int u = vec[t];
MaxR[u] = max(MaxR[vec[t+1]], Maxv[vec[t+1]]) + E[p[u]].len;
}
// Two-Pointers
PushMQ(0);
for(; (R+1) <= vec.size()-1 && Len + E[p[ vec[R] ]].len <= S; R++)
PushMQ(R+1), Len += E[p[vec[R]]].len;
while(true) {
// update ans
Ans = min(Ans, max3(MaxL[vec[L]], MaxR[vec[R]], Maxv[vec[MQ[Hd]]]));
if(R == vec.size()-1)
break;
else {
Len -= E[p[ vec[L] ]].len;
PopMQ(L);
++L;
if(L >= vec.size()) break;
for(; (R+1) <= vec.size()-1 && Len + E[p[ vec[R] ]].len <= S; R++)
PushMQ(R+1), Len += E[p[ vec[R] ]].len;
}
}
printf("%d", Ans);
}
int main() {
Init(); Work();
return 0;
}
