神仙DP题。
感谢_rqy的题解。如果以下内容有错误请指教。
题意
给出一个 $n \times 1001$ 的矩形,每个格子有 $q$ 的概率是安全的,要求选出一个与底边相邻且最大的安全矩形区域。求这个最大矩形区域面积恰好为 $k$ 的概率。
思路
建立状态转移方程
直接做根本做不了,考虑差分-前缀和之思想。
类似悬线法,我们把每根悬线加入状态。称下标 $n$ 对应的悬线长为从底部往上第一个危险格子下方的格子数目。
设状态 $f_k(i, j)$ 表示一个大小为 $i \times 1001$ 的泳池,底部所有的悬线长度 $\ge j$ ,且最大矩形面积 $< k$ 的概率。那么答案就是 $f_{k+1}(n, 0) - f_k(n, 0)$.(取 $>k$ 是为了避免负数下标)
决策是什么呢?先解决容易解决的边界情况。
$f(0, *) = 1; f(i, j) = 0 (\text{当 }ij \ge k)$,这是显然的。
再考虑一般情况的决策。我们不妨枚举从右往左第一个悬线长恰好为 $j$ 的位置 $p$ ,则其右边对应 $f(i-p, j+1)$。如图:
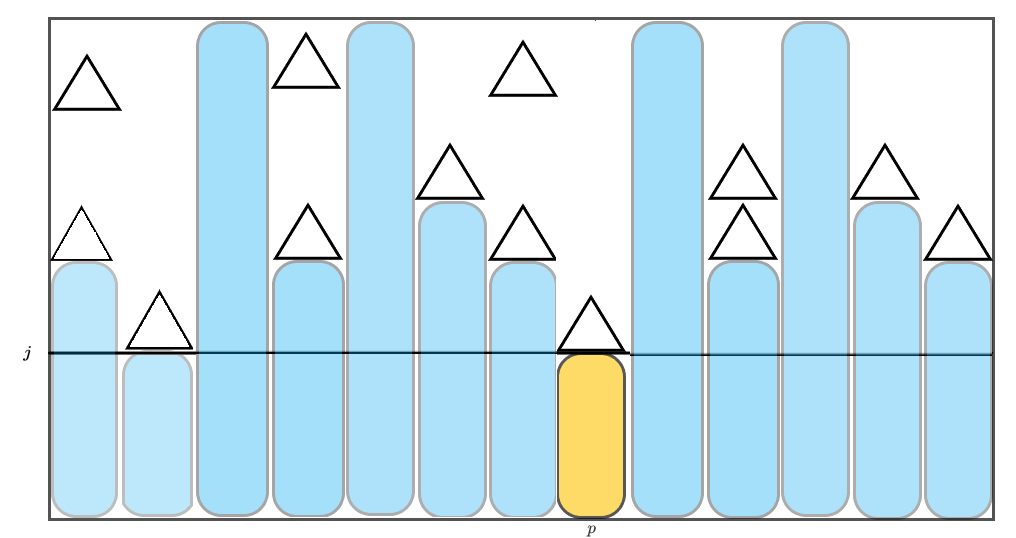
考虑到黄色位置左边仍然可能有位置悬线长恰好为 $j$ ,转移方程为: \(f(i, j) = \overbrace{f(i, j+1)}^{\text{最大子矩形高大于 } j\text{ ,即不存在 }p} + \overbrace{\sum_{p=1}^i \underbrace{f(i-p, j+1)}_{\text{黄色部分右边}} \times \underbrace{q^j(1-q)}_{p \text{位置}} \times \underbrace{f(p-1, j)}_{黄色部分左边}}^{\text{最大子矩形高等于} j} \:\:\:\:\: \text{when }ij < k\) 直接求,复杂度是 $O(kn)$ 的,可以获得 70 pts.
矩阵快速幂优化
$n \le 10^9, k \le 100$,显然地在提示矩阵快速幂。考虑到我们只需要 $f(*, 0)$,那么就令 $g_i = f(i, 0)$.
对于 $g_1 \sim g_k$ 的部分直接暴力算,有用的状态不超过 $O(n \sqrt{n})$ 个。对于 $i \ge k$ 的情况,显然有 $f(i, j) = 0$ $(j \ne 0)$.
于是:
\[\begin{align*} g_i = f(i, 0) &= f(i, 1) + \sum_{p=1}^i f(i-p, 1) \times (1-q) \times g_{p-1} \\ &= \sum_{p=i-k}^{i-1} f(i-p-1, 1) \times (1-q) \times g_{p} \\ &= \sum_{j=i-p=1}^k (1-q)f(j-1, 1) \times g_{i-j} \end{align*}\]可以看出这个是常系数齐次线性递推。构造转移矩阵进行优化:
\[\begin{bmatrix}g_1 \\ g_2 \\ \vdots \\ g_n\end{bmatrix}^T \times \begin{bmatrix} 0 & & & & & (1-q) f(k-1, 1) \\ 1 & & & & & (1-q) f(k-2, 1) \\ & 1 & & & & (1-q) f(k-3, 1) \\ & & 1 & & & (1-q) f(k-4, 1) \\ & & & \ddots & & \vdots\\ & & & & 1 & (1-q)f(0, 1) \end{bmatrix} = \begin{bmatrix}g_2 \\ g_3 \\ \cdots \\ g_{n+1}\end{bmatrix}^T\]这样做的复杂度是 $O(k^3 \lg n)$ ,可以获得 90pts.
利用多项式算法
这里取系数 $a_i = (1-q)f(i-1, 1)$ 即可。
实现
#include <bits/stdc++.h>
using namespace std;
namespace polynomial {
// 多项式大全略
}
using namespace polynomial;
int n, k, x, y, q, ans, v[MAXN + 10], p[MAXN + 10], c[MAXN + 10];
map<pair<int, int>, int> opt;
int dp(int i, int j) {
if(opt.count(make_pair(i, j)))
return opt[make_pair(i, j)];
else {
if(i == 0) return opt[make_pair(i, j)] = 1;
else if(i * j >= k || j > 1000) return opt[make_pair(i, j)] = 0;
else {
opt[make_pair(i, j)] = dp(i, j + 1);
for(int p = 1; p <= i; p++)
opt[make_pair(i, j)] = pls(opt[make_pair(i, j)], mul(dp(i - p, j + 1), mul(fpow(q, j), mul(dec(1, q), dp(p - 1, j)))));
return opt[make_pair(i, j)];
}
}
}
void solve(int x, int ret[]) {
static int a[MAXN + 10], tmp[MAXN + 10];
memset(ret, 0, sizeof(int) * (MAXN + 10));
ret[0] = 1;
memset(a, 0, sizeof(a)), memset(tmp, 0, sizeof(tmp));
a[1] = 1;
while(x > 0) {
if(x & 1) {
conv(k-1, ret, a, ret);
poly_div(2*k-2, k, ret, p, tmp, ret); // 模k次多项式,余式才为k-1次!!!
}
x >>= 1;
conv(k-1, a, a, a);
poly_div(2*k-2, k, a, p, tmp, a);
}
}
void work(int factor) {
for(int i = 0; i < k; i++) v[i] = dp(i, 0);
p[k] = 1;
for(int i = 1; i <= k; i++)
p[k - i] = mul(dec(q, 1), dp(i - 1, 1));
solve(n, c);
for(int i = 0; i < k; i++)
ans = pls(ans, mul(factor, mul(v[i], c[i])));
opt.clear();
}
int main() {
cin >> n >> k >> x >> y;
q = mul(x, mod_inv(y));
if(n <= 1000 && k <= 1000) {
k++; ans = pls(ans, dp(n, 0)); opt.clear();
k--; ans = dec(ans, dp(n, 0)); opt.clear();
} else {
k++; work(1);
k--; work(MOD-1);
}
cout << ans;
return 0;
}