A. Splits
考虑全部分成 $1$ 以及分成 $2, 1$ 两种情况,可以证明答案是 $n / 2 + 1$.
B. Messages
并不需要DP!贪心即可!
如果 $C - B > 0$,那么把所有的信件留到最后再看,否则一收到就看。
C. Alternating Sum
\[\begin{align*} \sum_{i=0}^n s_i a^{n-i} b^i &= \sum_{i=0}^{k-1}s_ia^{n-i}b^i + \sum_{i=k}^{2k-1}s_ia^{n-i}b^i + \cdots + \sum_{i=n-k+1}^ns_ia^{n-i}b^i \\ &= \sum_{i=0}^{k-1}s_ia^{n-i}b^i + \sum_{i=0}^{k-1}s_i a^{n-i-k} b^{i+k} + \cdots + \sum_{i=0}^{k-1}s_i a^{k-i-1} b^{i+n-k+1} \\ &= \left(\sum_{i=0}^{k-1}s_ia^{n-i}b^i\right) \cdot \left(1 + \left(\frac{b}{a}\right)^k + \left(\frac{b}{a}\right)^{2k} + \cdots + \left(\frac{b}{a}\right)^n \right) \end{align*}\]分 $b / a = 1$ 和 $b / a \neq 1$ 两种情况应用等比数列求和。
D. Destruction of a Tree
构造好题。
我们可以证明,如果一个树的点数目是偶数,那么答案一定是NO。
不妨设点数 $n$ 为偶数,则边数 $n-1$ 为奇数,但是每次删除度数为偶数的点的同时,只会删除偶数条边,所以肯定删不完。
反之,当点数为奇数的时候,一定可以完成删除。
考虑用 DFS 来完成整棵树的删除。
DFS 过程如下:
- 递归删除大小为偶数的子树
- 删除该节点
- 递归删除大小为奇数的子树
这样就可以删除整棵树。让我们用数学归纳法证明它。
当树中有 $1$ 个或者 $3$ 个节点的时候显然成立。
显然,如果要删除的子树有偶数个节点,那么它就一定有一个父亲。如果它的一个大小为偶数的子树可以被完全删除,那么它在此后就剩下偶数个节点(偶数-偶数=偶数),在除开它自己后剩下奇数个节点。由于剩下的子树大小都是奇数,所以剩下的子树个数也是奇数。考虑它的父亲后我们发现它的度数是偶数!于是可以删除。删除它后,对于它的奇数子树递归删除。
如果要删除的子树有奇数个节点,那么它要不然没有父亲,要不然父亲已经被删除。这样的话,删除了大小为偶数的子树后,就剩下了奇数个节点。如果除开它自己,剩下的节点数目为偶数。考虑到剩下的子树大小都为奇,剩下的子树数目必为偶,所以当前点可以删除。删除后对于奇数子树递归删除即可。
综上所述,命题得证。
E. Cutting Rectangles
又一个构造好题。
题意:给出一些小的矩形,每种 $w_i \times h_i$ 大小的矩形有 $c_i$ 个,问在不旋转的前提下能拼成多少个大小不同的大矩形。
(感谢 @Blue233333)
我们可以考虑先拼出一个 “Base Part”,再对它多次复制来构造出一个大矩形,像这样(怎么有点像 Windows 徽标……):
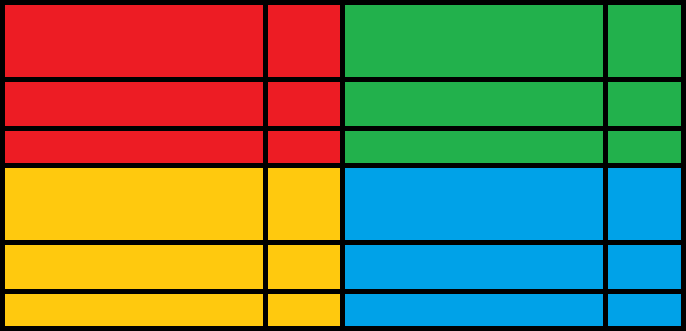
我们设 $\gcd_{c1, c2, \cdots, c_n} = G$.
多次复制的枚举过程并不难:枚举大矩形的长宽比即可。这一步的复杂度最坏是 $O(\sqrt{G})$.
再看如何构造 “Base Part”:只需要保证 $w$ 不同的时候,不同 $h$ 的小矩形个数成比例即可。
注意成比例的判断:
Hack Data:
4
1 2 2
1 3 3
2 2 4
2 3 6
成比例判断有问题的会输出 0,但是答案显然是 1.
最好是在下场比赛之前把这场的Div.1题都做完……不然要是上了 Candidate Master怎么办……