题意
给出一个 $P \times Q \times R$ 的长方体,横着切一刀,使得在满足相邻切点 $z$ 轴距离小于 $D$ 的前提下,切面权值和最小。
思路
题中是个显然的最小割模型,但是“某些点不能同时割”的限制比较棘手,不是很好处理……
尝试了几种建图方法,但都没办法证明正确性。看了题解才发现其中一种几乎就是正解……
对于最小割相关问题,思考的时候不应该套最大流的“容量”等概念,而要抓住割的性质:
- 割使得 $s-t$ 不连通
- 割把点划分为 2 个集合
其中,后者较容易从题中看出,从而建立出相应的模型。但是本题所应用的第一个性质就没有那么显然了。
我们紧扣第一个性质来设计模型。
割使得 $s-t$ 不连通 $\Leftrightarrow$ 使得 $s-t$ 连通的一定不是割
由此我们可以设法让某些点对应的边一定不会同时被割。方法就是加边,使得仅仅去掉那些点对应的边之后,图仍然连通(这样它们就不会一起选入最小割了)。
具体建图如下:
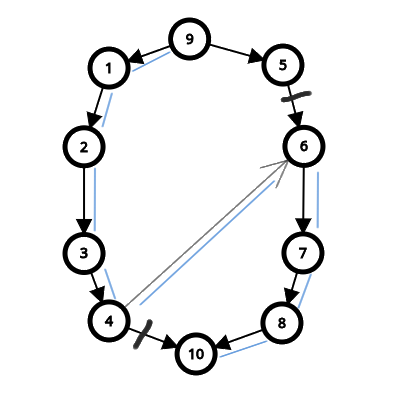
对于每个点 $(i, j, k)$, 我们从它向 $(i, j, k+1)$ 对应点连边。边权为该点的不和谐度。同时我们从它向 $(i’, j’ ,k-d)$ 对应点连边,权值为 $\infty$ 。我们考察割去 $(i, j, k)$ 以及 $(i’,j’,k-d-1)$ 对应边之后的情况。下图中有 $s=9, t=10$。假设 $d=2$ ,而我们想禁止 $3,5$ 号点对应的边,即 $<4,10>,<5,6>$ 同时选入割中。我们就连边 $<4, 6>$ ,权值无穷大。这样的话,即使我们移除了 $<4,10>, <5,6>$ 两条边,$s-t$ 通过蓝色路径仍然可以连通。
代码
#include <bits/stdc++.h>
#define rep(i, x) for(int i = 1; i <= (x); i++)
using namespace std;
const int MAXL = 40, MAXN = 1e5, MAXM = 1e6, INF = 0x3f3f3f3f;
const int di[] = { -1, 1, 0, 0 }, dj[] = { 0, 0, -1, 1 };
namespace Maxflow {
struct Edge {
int v, flow, cap, next;
};
int s, t, e_ptr = 1, head[MAXN+10]; Edge E[(MAXM+10)<<1];
int cur[MAXN+10], d[MAXN+10];
void AddEdge(int u, int v, int cap) {
E[++e_ptr] = (Edge) { v, 0, cap, head[u] }; head[u] = e_ptr;
E[++e_ptr] = (Edge) { u, 0, 0, head[v] }; head[v] = e_ptr;
}
bool BFS() {
queue<int> Q;
memset(d, 0xff, sizeof(d));
Q.push(s); d[s] = 0;
while(!Q.empty()) {
int u = Q.front(); Q.pop();
for(int j=head[u]; j; j=E[j].next) {
int v = E[j].v, f = E[j].flow, c = E[j].cap;
if(f < c && d[v] == -1) {
d[v] = d[u] + 1;
if(v == t) return true;
else Q.push(v);
}
}
}
return false;
}
int DFS(int u, int flow) {
if(u == t || flow == 0) return flow;
int res = flow;
for(int &j=cur[u]; j; j=E[j].next) {
int v = E[j].v, f = E[j].flow, c = E[j].cap;
if(d[v] == d[u] + 1) {
int aug = DFS(v, min(res, c-f));
E[j].flow += aug; E[j^1].flow -= aug;
res -= aug;
}
}
return flow - res;
}
int Dinic() {
int MaxFlow = 0, CurFlow = 0;
while(BFS()) {
memcpy(cur, head, sizeof(head));
while( (CurFlow = DFS(s, INF)) )
MaxFlow += CurFlow;
}
return MaxFlow;
}
}
int P, Q, R, D, V[MAXL+10][MAXL+10][MAXL+10];
inline int readint() {
int f=1, r=0; char c=getchar();
while(!isdigit(c)) { if(c=='-')f=-1; c=getchar(); }
while(isdigit(c)) { r=r*10+c-'0'; c=getchar(); }
return f*r;
}
inline int idx(int i, int j, int k) {
return (k-1) * P * Q + (i-1) * Q + j;
}
inline bool valid(int i, int j) {
return i >= 1 && i <= P && j >= 1 && j <= Q;
}
void Init() {
using namespace Maxflow;
P = readint(); Q = readint(); R = readint(); D = readint();
rep(k, R) rep(i, P) rep(j, Q) V[i][j][k] = readint();
s = MAXN - 1, t = MAXN;
rep(k, R-1) rep(i, P) rep(j, Q)
AddEdge(idx(i, j, k), idx(i, j, k+1), V[i][j][k]);
rep(i, P) rep(j, Q) {
AddEdge(s, idx(i, j, 1), INF);
AddEdge(idx(i, j, R), t, V[i][j][R]);
}
rep(i, P) rep(j, Q)
for(int k = D+1; k <= R; k++)
for(int dir = 0; dir < 4; ++dir) {
int ni = i + di[dir], nj = j + dj[dir];
if(!valid(ni, nj)) continue;
AddEdge(idx(i, j, k), idx(ni, nj, k-D), INF);
}
}
void Work() {
cout << Maxflow :: Dinic();
}
int main() {
Init(); Work();
return 0;
}