链接：Luogu-P1315
这个题目是在某模拟赛中看到的……并没有做过，当时认为是DP，没有注意到加速器会影响等车的时间，认为只影响坐车的时间。想到了差分。考试结束之前20分钟才发现不满足无后效性，于是完挂爆0。
分析
Why Greedy?
- DP的状态难以设计，而且无法转移
- 是序列问题，也没有明显的元素间关系
- 最小化旅行的时间，是最优化问题 最优化 $ \Rightarrow $ DP/贪心
既然DP不行，就只有贪心咯
切入问题
\[\text{旅行时间} \Rightarrow \begin{cases} \text { 等待时间 } \xleftarrow{ \text{取决于} } \begin{cases} \text { 最后到的人的到达时间 } \Leftarrow \text{不变}\\ \text { 车到达的时间 } \Leftarrow \text{受到加速器影响} \end{cases} \\ \text { 坐车时间 } \xleftarrow{ \text{缩短} } \text{加速器} ⇗ \text{提早} \end{cases}\]从上面的分析我们可以知道，问题的关键就在于加速器。确定了加速器，坐车时间和等待时间的变化就确定了。
分析贪心依据
加速器怎么影响坐车的时间呢？ 我们可以发现，对于一次“应用加速器”的过程，如果不考虑最后到的人到达时间的影响，在加速的边右边的点下车的人时间会变优。对每个人的优化效果是相同的。
如上图，绿色块代表连接两个点的边，点未画出。对于红色箭头代表的人，他的坐车时间缩短了；而对于蓝色箭头代表的人，他的等待时间也缩短了。
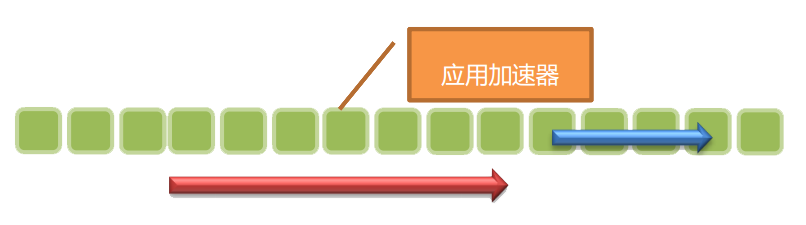
注意，加速器的优化效果是有限的：如果记汽车在站台 $i$ 停车的时间为 $Bus_i$， 该站最后一个到站台的人到达时间为$Last_i$， 从应用位置开始往右，找到的第一个满足 $ Bus_i \leq Last_i $ 的点即为优化效果的终止点。
那么在哪里使用加速器呢？有了优化范围（应用点到终止点）和优化的策略（最大化优化人数），就可以贪心了：首先预处理出每个站点下车的人数以及前缀和，以及不用加速器时到每个站的时间（递推），然后比较每个点，找出优化人数即可。
可能会想到一种错误的贪心，即对于每个极大的优化范围（两侧都是终止点）只用区间最左点更新最值。似乎是正确的，但是没有考虑边权非负的限制！ 对于有多个点取得最大优化人数的情况，任选一个装加速器即可。
代码
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 1000, MAXM = 10000;
int N, M, K, Ans, D[MAXN+10], T[MAXM+10], A[MAXM+10], B[MAXM+10],
Sum[MAXN+10], Last[MAXN+10], Bus[MAXN+10], Div[MAXN+10];
void PrepBus() {
for(int i=2;i<=N;i++)
Bus[i] = max(Bus[i-1],Last[i-1]) + D[i-1];
}
void Init() {
scanf("%d%d%d",&N,&M,&K);
for(int i=1;i<=N-1;i++) scanf("%d",&D[i]);
for(int i=1;i<=M;i++)
scanf("%d%d%d",&T[i],&A[i],&B[i]);
for(int i=1;i<=M;i++) {
Sum[B[i]]++; Last[A[i]]=max(Last[A[i]],T[i]);
}
for(int i=1;i<=N;i++)
Sum[i]+=Sum[i-1];
PrepBus();
}
void Work() {
Div[N] = N; Div[1] = 1;
for(int p=1;p<=K;p++) { //当前要用掉第i个加速器
int maxp=0, maxv=0;
for(int i=N-1; i>=1; i--) {
if(Bus[i] <= Last[i]) Div[i]=i;
else Div[i] = Div[i+1];
}
for(int i=N; i>=2; i--) //左侧放加速器
if(Sum[Div[i]] - Sum[i-1] > maxv && D[i-1] > 0) //注意读题：边权非负，则要装加速器的边的权值为正
maxv=Sum[Div[i]] - Sum[i-1], maxp=i;
D[maxp-1]--;
PrepBus();
}
for(int i=1;i<=M;i++) Ans+=Bus[B[i]]-T[i];
printf("%d",Ans);
}
int main() { Init(); Work(); }
