链接:Luogu-P1417
思路
看上去是一个01背包,不过价值随着时间的推移而改变,怎么办?
先考虑2个物品的情况,即进行基于交换的贪心。时间足够的时候,到底是先取物品1再取物品2,还是先取物品2再取物品1。如果考虑清楚了2个物品的情况,就可以进行排序,再利用动态规划得解。
实际上,如果设当前处在时刻$t_0$,两个物品的各个参数(见题)分别为$a_1,b_1,c_1$和$a_2,b_2,c_2$,则先取第一个物品更优,当且仅当有$b_1 c_2>b_2 c_1$
证明:设第一个物品先取时,两个物品总价值为$idx_1$;第二个物品先取时,两个物品总价值为$idx_2$。
则有:
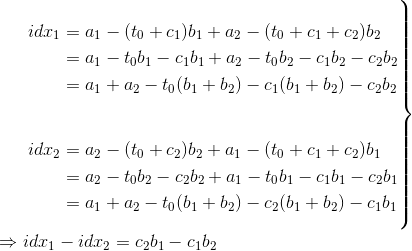
于是$idx_1>idx_2 \Leftrightarrow b_1c_2>b_2c_1$。按照这个排序,即可保证同时取得某些物品的时候,取得的价值是最优的。
然后跑01背包就行。
实现
注意01背包初始化为0,因为当一道菜的价值为负数的时候,完全可以不做。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 50, MAXT = 100000;
struct Food{
int a,b,c;
} W[MAXN+10];
int T,N;
LL opt[MAXT+10];
bool cmp(const Food& lhs,const Food& rhs){ return lhs.b*rhs.c>rhs.b*lhs.c; }
inline void Init(){
scanf("%d%d",&T,&N);
for(int i=1;i<=N;i++)
scanf("%d",&W[i].a);
for(int i=1;i<=N;i++)
scanf("%d",&W[i].b);
for(int i=1;i<=N;i++)
scanf("%d",&W[i].c);
}
inline void Work(){
sort(W+1,W+1+N,cmp);
for(int i=N;i>=1;i--) //先拿的物品在后拿的基础上更新
for(int j=1;j<=T-W[i].c+1;j++)
opt[j]=max(
opt[j], //注意乘法溢出↓
opt[j+W[i].c]+W[i].a-(j+W[i].c-1)*((LL)W[i].b)
);
printf("%lld",opt[1]);
}
int main(){
Init();
Work();
return 0;
}