链接：Luogu-P1736
题目大意
有一个$n \times m$的矩阵，要在里面寻找一个尽可能大的正方形，使得这个正方形某条对角线上都是1，其他地方都是0。求这个正方形对角线长。
思路
注意到求的是正方形，所以是裸的二维平面DP。对此类问题，画出图像，定义状态为以某个位置为右下角的最大合法正方形；再把“障碍方格”绕着可能影响转移的位置移动即可找出转移。
如本题，先考虑主对角线的情况。定义状态$f(i,j)$ : 以$(i,j)$ 为右下角的最大合法正方形。
如果$(i,j)$本身不是1，$f(i,j)=0$。如果它本身是1，情况如图。对于图中所有标有*的方块，如果都是0，显然就直接有$f(i,j)=f(i-1,j-1)+1$。如果其中存在一个1，那么它就破坏了本来可能形成的，边长为 $f(i-1,j-1)+1$ 的新正方形。换句话说，它就是个“障碍方格”，而* 位置就是可能影响转移的位置。
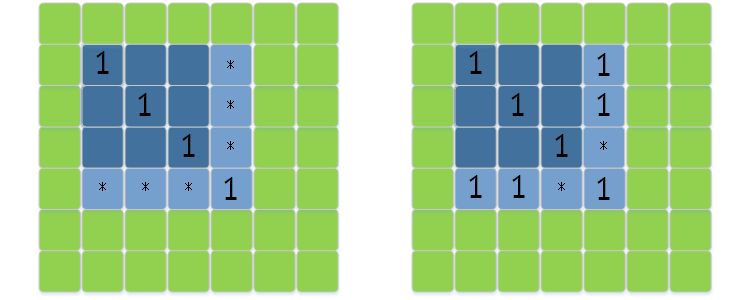把它在所有的*中移动，我们发现，只需要考虑离当前$(i,j)$在向左和向上方向最近的一个 1 的位置即可，而这个可以递推求得。
综合考虑三者可以得到： $f(i,j)=\min\{ a,b, f(i-1,j-1)+1 \}$
其中$a,b$为从$(i,j)$出发向左向上分别至少走多少步可以到达一个1（不考虑本身）。
至于副对角线，可以重新定义一个类似的状态，也可以把矩阵“翻折”一下，把原矩阵的第$j$列放到新矩阵的第$m-j+1$列，这样就转化为关于主对角线的问题了。
时间复杂度是$O(nm)$。
代码
注意递推的边界值，尤其是如果你针对副对角线重新定义了状态的话。
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
#define CLEAR(x) memset(x,0,sizeof(x))
using namespace std;
const int MAXN = 2500;
int N,M,Ans,W[MAXN+2][MAXN+2],opt[MAXN+2][MAXN+2],f[MAXN+2][MAXN+2],g[MAXN+2][MAXN+2];
//对点(i,j),f是往左最近的一个'1'，g是往上最近的一个'1'。不包括(i,j)本身。
inline int readint(){
int f=1,r=0;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){r=r*10+c-'0';c=getchar();}
return f*r;
}
inline void solve(){
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++) {
f[i][j]=f[i][j-1]+1;
g[i][j]=g[i-1][j]+1;
if(W[i][j]){
opt[i][j]=min(min(f[i][j],g[i][j]),opt[i-1][j-1]+1);
f[i][j]=g[i][j]=0;
}
Ans=max(Ans,opt[i][j]);
}
}
int main(){
N=readint(); M=readint();
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)
W[i][j]=readint();
solve();
for(int j=1;j<=M/2;j++)
for(int i=1;i<=N;i++)
swap(W[i][j],W[i][M-j+1]);
CLEAR(opt);CLEAR(f);CLEAR(g);
solve();
printf("%d\n",Ans);
}
