题目链接：CodeVS 3287
题意：给出一张无向图，每条边有一个边权，图上可以有重边，没有自环。求这张图上两点$u$,$v$之间所有路径上最小权值的最大值。若不能互相到达输出-1。
1.审题
1. 显然，无向图不一定是连通图，于是两点之间若要互相到达，必须在同一连通子图上。
2. 最小权值的最大值：图上$u$,$v$两点间有着多条路径，需要找到一条路径，这条路径上所求的权值最小的边最大。
2.思路分析
对于 30%的数据，0 < n < 1,000，0 < m < 10,000，0 < q < 1,000；
对于 60%的数据，0 < n< 1,000，0 < m < 50,000，0 < q < 1,000；
对于 100%的数据，0 < n < 10,000，0 < m < 50,000，0 < q < 30,000，0 ≤ z ≤ 100,000。
- 暴力DFS穷举$u$,$v$连通性以及所有路径上每一条边？ 最坏时间复杂度为 $O((n+m)q)$ → 30pts (如果时间复杂度算错了，请回复指教，谢谢 =.=）
- 尝试把问题转换为以某一种次序加入边；加入了某一条边之后，所查询的两点由不连通变为连通。
以什么顺序加入呢？考虑常见的升序/降序两种选项。
要满足“最小权值的最大值”，就要满足加入的边权值小于所有已加边，而且加入的边权值在满足题意的基础上尽可能大，也就是说选择降序排序。
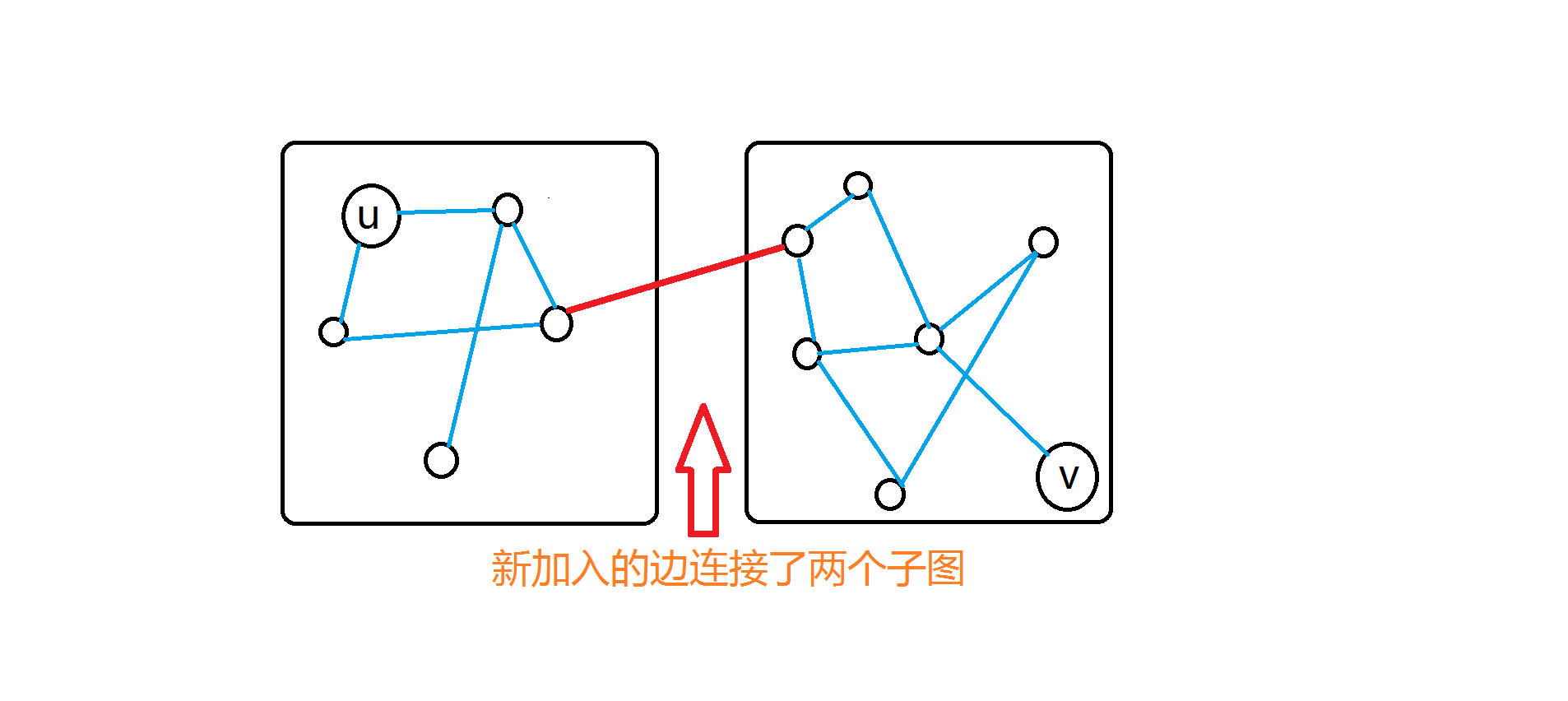如上图。对于某一个询问，逐一加入图中每一条边，用并查集维护连通性。
若某条边连接前， $u$ 与 $v$ 分属不同集合，连接后，所查询的两点并入了同一个集合，那么原来 $u$ , $v$ 所在的子图就连通了。须证明这条边为可行的权值最大的最小边。
这条边连接两个子图，即这条边为桥，那么边 $(u,v)$ 必然在 $u$ 到 $v$ 的路径上；
这条边权值小于所有已加边，于是必为路径上最小边；
若答案的权值大于这条边，由于答案能连通两个子图，且按照降序，在选择它之前答案已经选择，那么两个子图就已经被已经加入的答案边（图中的蓝色边之一）连通了，与题设“此边连接前，$u$ 与 $v$ 分属不同集合”矛盾。 综上，这样的一条边必为答案。
时间复杂度为 $O(mq)$ →60pts - 遇到图上查询，要考虑到转为某种生成树进行处理
转化成什么生成树呢？
其实从60分解法中我们可以猜测，应该转为最大生成树。
60分解法中，完全可以加入添加边时的判断，只有这条边所连的两点分属不同集合，才予以链接，也就是采用类似Kruskal算法的策略，不加入两个端点属于同一个集合的边。e.g.图中最左侧的蓝色边。这样并没有改变原图的连通性，也不影响“加边后由不连通变为连通”的情况。显然，60分解法中的证明过程仍然成立，也就是说，答案在求出的最大生成树上。
注意，此图不一定为连通图！于是构造出的实际上是最大生成森林。对森林中每棵最大生成树，进行倍增LCA的处理，或者使用树链剖分，即可快速求出树上路径上的最小权值。
时间复杂度为 $O((m+n+q)\log(n))$ →100pts
3.60分实现
有两种实现方式
1. 每建一条边，就把所有的查询都走一遍，如果符合题意就记录答案。
2. 针对每个查询，逐一建边，然后清空已建的边，再进行下个查询。
显然，2中清空并查集的操作，对于每次查询都需进行，复杂度太高，于是应该采用1。 代码：
#include<bits/stdc++.h>
#define REP(i,n) for(int i=0;i<n;i++)
#define REP1(i,n) for(int i=1;i<=n;i++)
using namespace std;
struct Edge{
int u,v,len;
friend bool operator>(const Edge &a,const Edge &b){
return a.len>b.len;
}
};
struct Query{
int x,y;
};
int N,M,Q,fa[1010],ans[1010];
Edge vec[50010];
Query q[1010];
inline void Init(){
REP1(i,N) fa[i]=i;
}
inline int GetFather(int x){
if(fa[x]==x) return x;
else return fa[x]=GetFather(fa[x]);
}
inline void Union(int x,int y){
int t1=GetFather(x),t2=GetFather(y);
fa[t1]=t2;
}
int main(){
scanf("%d %d",&N,&M);
REP(i,M)scanf("%d %d %d",&vec[i].u,&vec[i].v,&vec[i].len);
scanf("%d",&Q);
REP(i,Q)scanf("%d %d",&q[i].x,&q[i].y);
sort(vec,vec+M,greater<Edge>());
Init();
REP(i,M){
int u=vec[i].u,v=vec[i].v,len=vec[i].len;
Union(u,v);
REP(j,Q){
int x=q[j].x,y=q[j].y;
if(!ans[j] && (GetFather(x)==GetFather(y)))
ans[j]=len;
}
}
REP(i,Q)
if(!ans[i]) printf("-1\n");
else printf("%d\n",ans[i]);
return 0;
}
4.100分实现
-
还记得无向连通图的Kruskal算法吗？对于无向连通图，我们可以采用一个常数优化。当有 n-1 条边加入最小生成树之后，就不再需要继续运行算法，因为一棵有 $n$ 个节点的树含有 $n-1$ 条边。 对于 一般的无向图 ，Kruskal算法仍然可以求出每一棵子树的最小生成树，但是此时就不需要，也没必要采用上述优化。直接让Kruskal算法处理完所有的边即可。
-
使用两个并查集，一个用于判断连通性，一个用于建立最大生成树。技巧：不用写两套并查集的函数，只需向函数中传入fa数组的指针即可。类似的技巧常用于Treap等其他数据结构。 代码：
#include <bits/stdc++.h>
#define MAXM 50000
#define MAXN 10000
#define INF 0x3f3f3f3f
#define CLEAR(x) memset(x,0,sizeof(x))
#define SETNINF(x) memset(x,0xCF,sizeof(x))
#define SETINF(x) memset(x,0x3F,sizeof(x))
#define UpMin(x,t) (x=min(x,t))
#define REP(i,n) for(int i=0;i<n;i++)
#define REP1(i,n) for(int i=1;i<=n;i++)
using namespace std;
struct Edge{
int u,v,len;
bool operator>(const Edge& ed)const{
return len>ed.len;
}
};
struct Edge2{
int v,len,next;
};
int N,M,Q,fa[2*MAXN+10],fac[2*MAXN+10];
int e=1,head[2*MAXN+10];
int dep[2*MAXN+10],anc[2*MAXN+10][25],minn[2*MAXN+10];
Edge a[2*MAXM+10];
Edge2 E[4*MAXN+10];
void addedge(int u,int v,int len){
E[e]=(Edge2){v,len,head[u]};head[u]=e++;
E[e]=(Edge2){u,len,head[v]};head[v]=e++;
}
inline int readint(){
int f=1,r=0;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){r=r*10+c-'0';c=getchar();}
return f*r;
}
int GetFather(int x,int* fa){
if(fa[x]==x) return x;
else return fa[x]=GetFather(fa[x],fa);
}
inline void Union(int x,int y,int* fa){
int t1=GetFather(x,fa),t2=GetFather(y,fa);
fa[t1]=t2;
}
inline void DoMaxSpTree(){
REP1(i,N) fa[i]=i;
sort(a,a+M,greater<Edge>());
REP(i,M){
int u=a[i].u,v=a[i].v,len=a[i].len;
if(GetFather(u,fa)!=GetFather(v,fa)){
addedge(u,v,len);Union(u,v,fa);
}
}
}
void Dfs(int u){
REP1(i,22){
anc[u][i]=anc[anc[u][i-1]][i-1];
minn[u][i]=min(minn[u][i-1],minn[anc[u][i-1]][i-1]);
}
for(int j=head[u];j;j=E[j].next){
int v=E[j].v,len=E[j].len;
if(v==anc[u][0]) continue;
dep[v]=dep[u]+1;
anc[v][0]=u;minn[v][0]=len;
Dfs(v);
}
}
int Query(int u,int v){
int ans=INF;
if(dep[u]<dep[v])swap(u,v);
for(int i=22;i>=0;i--)
if(dep[anc[u][i]]>=dep[v]){
UpMin(ans,minn[u][i]);u=anc[u][i];
}
if(u==v) return ans;
for(int i=22;i>=0;i--)
if(anc[u][i]!=anc[v][i]){
UpMin(ans,minn[u][i]);UpMin(ans,minn[v][i]);
u=anc[u][i];v=anc[v][i];
}
UpMin(ans,minn[u][0]);UpMin(ans,minn[v][0]);
return ans;
}
inline void InitST(){
SETINF(minn);
set<int> ts;int p;
REP1(i,N)
if(!ts.count(GetFather(i,fac)))
ts.insert(GetFather(i,fac));
for(set<int>::iterator i=ts.begin();i!=ts.end();i++){
dep[*i]=1;Dfs(*i);
}
}
int main(){
N=readint();M=readint();
REP1(i,MAXN) fac[i]=i;
REP(i,M){
int u,v,c;u=readint();v=readint();c=readint();
a[i]=(Edge){u,v,c};
Union(u,v,fac);
}
DoMaxSpTree();
InitST();
Q=readint();
while(Q--){
int x,y;x=readint();y=readint();
if(GetFather(x,fac)==GetFather(y,fac))
printf("%d\n",Query(x,y));
else printf("-1\n");
}
return 0;
}
5. 小结
本题是2013年NOIP提高组最后一题，考察了并查集，生成树，倍增等知识点。 有以下几点值得注意：
- 审题要周全。一定要注意，题中的图不一定是连通图，并进行判断。
- 有一定编程复杂度，需要多次检查，尤其要注意倍增查询部分 u , v 不可写反！可以先写出60pts的程序，再与100pts程序对拍。 不要过度相信自己手画的随机数据，应该使用数据生成器。
题解就写到这里啦。 如果有任何问题或者本文有什么错误请在评论区指出。 求各位神犇轻喷 orz
9e544e09c0fcabdc07ed5667c98147efa64dac0a
