第一次学是 1 月份雅礼集训的时候……不过太久没用已经忘了= = 而且当时理解也不是很到位。
要省选了,得复习一下,顺便把坑填起来。
约定: $\Sigma$ 表示字符集大小,$T$ 为模板集合,$S$ 为母串,我们的目标是在母串中找出模板。
Trie
就是把各个字符串相同的前缀合并形成的树。比方说 $\mathtt{[“his”, “she”, “hers”, “is”]}$ 的 Trie 长这样:
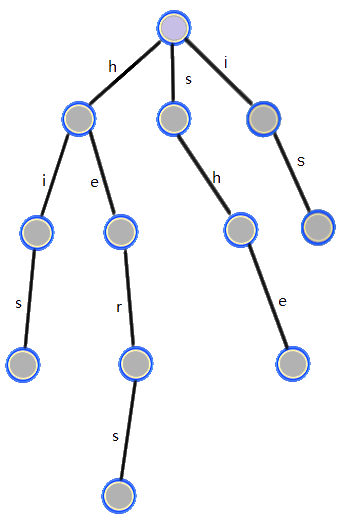
把一个串插入 Trie 中代码如下。为了处理重复串, val[] 记录某个串在插入了 Trie 的串中出现了多少次。std::unordered_map<string, int> ms 用来记录每个串对应 Trie 中哪个点。
int sz, val[MAX_NODE+10], ch[MAX_NODE+10][SIGMA+10];
std::unordered_map<string, int> ms;
inline int idx(int c) { return c - 'a' + 1; }
void insert(char *str) {
int len = strlen(str), u = 0;
for(int i = 0; i < len; i++) {
int c = idx(str[i]);
// 建立新点,再向前走一步
if(!ch[u][c]) ch[u][c] = ++sz;
u = ch[u][c];
}
++val[u];
ms[string(str)] = u;
}
AC 自动机
用来在某个母串中找出出现的模板串。为了方便叙述,设 $S = \mathtt{“hishers”}$ 。
考虑在Trie上面行走,一个一个地匹配模板串。不能直接沿用在 Trie 中查找的过程,因为有2个问题摆在面前:
- 某个模板串 $T_i$ 的后缀是另一个模板串 $T_j$ 的前缀。这样的话匹配完成 $T_i$ 后, $T_j$ 也完成了部分的匹配,应该跳到 $T_j$ 看匹配完成没有。如 $T_i = \mathtt{“his”}, T_j = \mathtt{“she”}$ 。
- 某个模板串失配了,但是可能匹配上前缀相同的另一模板。如 $\mathtt{“his”}$ 和 $\mathtt{“hers”}$ 。
同时,上述 1 还有一种特例:
- 某个模板串 $T_i$ 的后缀等于另一个模板串 $T_j$ 。如 $\mathtt{“his”}$ 和 $\mathtt{“is”}$ 。
失配边
为了解决上面的问题,就要充分利用已匹配部分的信息。我们给 Trie 添加一些边来进行上述转移。
- 对于 1 ,从 $T_i$ 的结尾点向 $T_j$ 的相同前缀的结尾点连边
- 对于 2 ,从 $T_i$ 的失配点向 $T_j$ 当前匹配到的点连边(因为匹配 $T_i$ 的过程中 $T_j$ 也部分匹配)
上述两个对应的边集合称为失配边。特别地,如果不存在满足条件的 $T_j$ ,失配边指向 Trie 的根。
如图。为了清晰,只画出了部分失配边,且失配边指向根的均未画出。
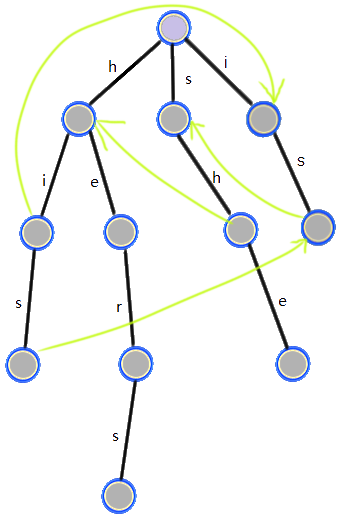
不难想到,如果由浅到深逐层遍历 Trie ,第 $i$ 层的失配边可以由第 $i-1$ 层推出,即由图中黄色边推出绿色边:
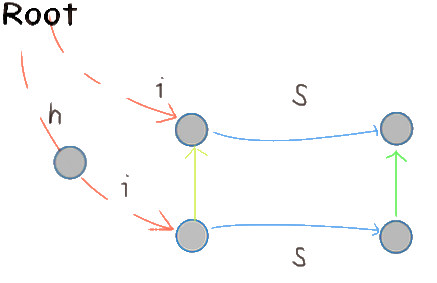
同时为了加速匹配,我们维护后缀链接,即从某点出发,沿着失配边走,走到的第一个单词节点。
代码如下:
int f[MAX_NODE+10], last[MAX_NODE+10];
void get_fail() {
std::queue<int> Q;
for(int c = 1; c <= SIGMA; c++) if(ch[0][c]) {
int v = ch[0][c];
f[v] = last[v] = 0; Q.push(v);
}
while(!Q.empty()) {
int u = Q.front(); Q.pop();
for(int c = 1; c <= SIGMA; c++) {
int v = ch[u][c];
if(!v) { ch[u][c] = ch[f[u]][c]; continue; } // 利用失配边信息,把不存在的边补上,见下文
Q.push(v);
int u2 = f[u];
while(u2 && !ch[u2][c]) u2 = f[u2];
f[v] = ch[u2][c];
last[v] = val[f[v]] ? f[v] : last[f[v]];
}
}
}
“把不存在的边补上”是怎么回事呢?考虑某个点没有母串当前位置字符对应儿子的情况,也就是不存在上图中下面一条蓝色边。在匹配的时候应该沿着s失配边,也就是左边的黄边走。为了避开这个过程,我们补上这条边,也就是连接左下角点到右上角点的边。这样走失配边的操作就可以省略了。
匹配
这个就不用解释了,沿着边走就可以了。也许当前点不是匹配点,但是后缀链接上有匹配点,要判断。注意:一定要先走一步再判断是否找到!!!不然最后一个位置无法匹配!!!
void found(int u) {
for(; u; u = last[u])
found_cnt[u] += val[u];
}
void search(char *str) {
int len = strlen(str), u = 0;
for(int i = 0; i < len; i++) {
int c = idx(str[i]);
u = ch[u][c];
if(val[u]) found(u);
else if(last[u]) found(last[u]);
}
}
例题
其实AC自动机不过就是个状态转移图而已,图论的玩法一般也都适用。
单串的多模式匹配这种板子题就不放了。
[POI2000]病毒
建立了AC自动机之后就是要判断有没有从0可以到达的环。sb的我最开始居然还在BFS……过了好久我才想起来有拓扑排序这种东西= = 拓扑排序即可。存在拓扑序输出 “NIE”,否则输出 “TAK”.
有向无环图存在拓扑序。如果无法找出拓扑序,说明图不是有向无环图。——刘汝佳《算法竞赛入门经典》
(以及编译输出文件名写成了源代码,直接把源代码覆盖了……重新打了一遍……省选的时候,一定不能犯这样的低级错误!写完了就用GUI备份一份,不要用rm,mv,cp什么的!编译最好也别敲命令!用gedit的External Tool!)