参考了这个题解,虽然有错误,但是讲的很不错。
感觉网上某些斜率优化的题解就是混的,没有严谨的证明,所以我试着证明一下= =
如果证明错了就使劲喷我好了= =
斜率优化
HDU3507
题意
把一个序列 ${c_n}$ 划分成若干份,每份的代价为 $\left( \sum c_i \right)^2 + M$. 最小化总代价和。
思路
$f(i)$ 表示前 $i$ 个的最小总代价和。
于是 $f(i) = \min_{0 \le j \le i-1} \{ f(j) + \left(\sum_{j+1 \le k \le i} c_i\right)^2 + M \}$. 边界为 $f(0) = 0$. 但是复杂度太高,无法胜任题中数据范围。考虑进行优化。看到 $\min$ ,联想到单调数据结构。
假设在 $j = \alpha$ 时取值优于 $j = \beta$ ,且 $\alpha > \beta$ , 而 $\{c_n\}$ 前缀和为 $\text{sum}(i)$ ,就有: \(\newcommand{\sumc}{\text{sum}} \begin{align*} f(\alpha) + \sumc^2(\alpha) - 2\sumc(\alpha) \sumc(i) + \sumc^2(i) + M &< f(\beta) + \sumc^2(i) - 2 \sumc(\beta) \sumc(i)+ \sumc^2(\beta) + M \\ f(\alpha) + \sumc^2(\alpha) - 2\sumc(\alpha)\sumc(i) &< f(\beta) + \sumc^2(\beta) - 2\sumc(\beta)\sumc(i) \\ \end{align*}\)
令 $ y_{\alpha} = f(\alpha) + \sumc^2(\alpha), y_{\beta} = f(\beta) + \sumc^2(\beta), x_{\alpha} = 2\cdot \sumc(\alpha), x_{\beta} = 2 \cdot\sumc(\beta)$ ,则有:
\[\begin{equation*} y_{\alpha} - y_{\beta} < (x_{\alpha} - x_{\beta}) \cdot \sumc(i) \end{equation*}\]显然,$\sumc(x)$ 关于 $x$ 单调递增,于是当 $\alpha > \beta$ 时,$\sumc(\alpha) \ge \sumc(\beta)$ ,斜率存在时,有:
\[\frac{y_{\alpha} - y_{\beta}}{x_{\alpha} - x_{\beta}} < \sumc(i)\]由于 $x_i$ 单调递增,除数大于0,不等号不变号。上面的式子为斜率形式,我们可以在坐标系中画出对应的点。
不妨记左侧为 $K(\alpha, \beta)$. 同理可得,上式取 $\ge$ 时,满足在 $j=\beta$ 时取值优于 $j=\alpha$.
我们下面就证明一个一般的结论。
对于形如 $f(i) = \min\{f(j) + g(i, j) \vert j < i\}$ 形式的状态转移方程,假如 $\alpha < \beta < \gamma$ ,而且化简后满足 $\frac{y_{\alpha} - y_{\beta}}{x_{\alpha} - x_{\beta}} < A(i)$ ,则只要 $x_i$ (非严格地)单调递增,而且 $K(\beta,\alpha) \ge K(\gamma, \beta)$ ,那么在求 $f(i)$ 时,一定不会在 $j = \beta$ 处取得最小值。
- 当 $K(\gamma, \beta) < A(i)$ 时:由上式定义知,取得 $j = \gamma$ 优于 $j = \beta$ . 所以不会在 $j = \beta$ 取得最小值。
- 当 $K(\gamma, \beta) \ge A(i)$ 时:取得 $j=\beta$ 优于 $j = \gamma$ ,但是取得 $j=\alpha$ 优于 $j = \beta$ ,所以仍然不会取得 $j = \beta$ .
综上所述,一定不会在 $j = \beta$ 处取得最小值,命题得证。
因此可以移除 $j = \beta$ 对应的点。于是可行的决策点一定满足斜率逐渐增大,即形成上凸壳。如图。
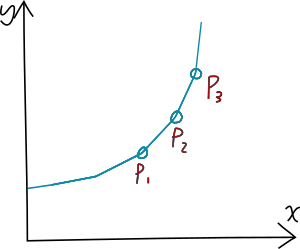
用单调队列维护凸壳。维护单调队列相邻元素之间的斜率单调递增,即:对于任意 2 个相邻元素(自然,也就是 $c_i$ 中的下标)$A, B$ ,如果队列中 $A$ 在 $B$ 前面,一定有从队首到队尾 $K(B, A)$ 单调递增。求解的时候首先检查队首的斜率是否小于 $\sumc(i)$ ,大于的话,说明队首比它后面的所有元素更优,于是队首为决策点,求解 $f(i)$,反之队首出队,因为由上述转移方程,如果这时候队首不是最优决策点,以后 $\sumc(i) - \sumc(j)$ 越来越大(由 $A(i)$ 单调递增性质),更不可能是最优决策点。当然,对于一般的斜率优化 DP,如果 $A(i)$ 不是单调递增的,就不能直接让队首出队,应该在凸包上二分。
代码
注意避免除法。就算是队列末尾的 2 个元素对应斜率等于带插入元素和最后一个元素的斜率,也要继续弹出。
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5e5;
int N, M, Sum[MAXN+10], opt[MAXN+10];
inline int readint() {
int f=1, r=0; char c=getchar();
while(!isdigit(c)) { if(c=='-')f=-1; c=getchar(); }
while(isdigit(c)) { r=r*10+c-'0'; c=getchar(); }
return f*r;
}
inline bool Init() {
if(scanf("%d%d", &N, &M) == EOF)
return false;
for(int i = 1; i <= N; i++)
Sum[i] = readint() + Sum[i-1];
return true;
}
int Hd = 1, Tl = 0, Q[(MAXN+10)<<1];
inline int GetY(int i) { return opt[i] + Sum[i] * Sum[i]; }
inline int GetX(int i) { return 2 * Sum[i]; }
inline void Work() {
Hd = 1, Tl = 0;
opt[0] = 0; Q[++Tl] = 0;
for(int i = 1; i <= N; i++) {
while(Tl - Hd + 1 >= 2 &&
(GetY(Q[Hd+1]) - GetY(Q[Hd])) < Sum[i] * (GetX(Q[Hd+1]) - GetX(Q[Hd])))
++Hd;
int j = Q[Hd];
opt[i] = opt[j] + (Sum[i] - Sum[j]) * (Sum[i] - Sum[j]) + M;
while(Tl - Hd + 1 >= 2 &&
(GetY(Q[Tl]) - GetY(Q[Tl-1])) * (GetX(i) - GetX(Q[Tl])) >=
(GetY(i) - GetY(Q[Tl])) * (GetX(Q[Tl]) - GetX(Q[Tl-1])))
--Tl;
Q[++Tl] = i;
}
printf("%d\n", opt[N]);
}
int main() {
while(Init())
Work();
return 0;
}
BZOJ1010
题意
略。
思路
DP方程:$f(i) = \min\{f(j) + \left(\left(i - (j+1)+\sum_{j+1 \le k \le i}c_k\right) - L\right)^2 \vert 0 \le j \le i-1\}$
同样应用斜率优化:设在 $j=\alpha$ 处取值优于 $j=\beta$ ,且 $\alpha > \beta$ . 设 $\sumc(i) = \sum_{1 \le k \le i}c_k$ .
则有: \(f(\alpha) + \left(i - \alpha - 1 + \sumc(i) - \sumc(\alpha)-L\right)^2 < f(\beta) + \left(i - \beta - 1 + \sumc(i) - \sumc(\beta)-L\right)^2\) 暴力展开,消掉小于号两边的相同项,再合并,并且把带有 $\alpha, \beta$ 的项移到式子同一侧,只有 $i$ 的移动到另一侧(非常难算,堪比解析几何……),就有:
\[f(\alpha) - f(\beta) +\alpha^2 - \beta^2 + 2(L+1)(\alpha - \beta + \sumc(\alpha) - \sumc(\beta)) + \sumc^2(\alpha) - \sumc^2(\beta) + 2\alpha \cdot \sumc(\alpha) \\- 2\beta \cdot sum(\beta) < 2i \cdot (\alpha - \beta) + 2\sumc(i)\cdot[\sumc(\alpha) - \sumc(\beta)] + 2i \cdot [\sumc(\alpha) - \sumc(\beta)] + 2\sumc(i) \cdot(\alpha - \beta)\]令
\[\begin{align*} y_{\alpha} = f(\alpha) + \alpha^2 + (2L+2)[\alpha+\sumc(\alpha)] &+ \sumc^2(\alpha) + 2\alpha \cdot\sumc(\alpha), x_{\alpha} = \alpha + \sumc(\alpha),\\ y_{\beta} = f(\beta) + \beta^2 + (2L+2)[\beta+\sumc(\beta)] &+ \sumc^2(\beta) + 2\beta \cdot\sumc(\beta),x_{\beta} = \beta + \sumc(\beta) \end{align*}\]则有
\[\begin{equation*} \frac{y_{\alpha} - y_{\beta}}{x_{\alpha} - x_{\beta}} < 2[i + \sumc(i)] \end{equation*}\]因为右式满足单调递增,由斜率优化的正确性(上题已证),可以直接单调队列维护凸壳求解。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int64;
const int MAXN = 5e4;
int64 N, L, Sum[MAXN+10], opt[MAXN+10];
inline int readint() {
int f=1, r=0; char c=getchar();
while(!isdigit(c)) { if(c=='-')f=-1; c=getchar(); }
while(isdigit(c)) { r=r*10+c-'0'; c=getchar(); }
return f*r;
}
void Init() {
N = readint(); L = readint();
for(int i = 1; i <= N; i++)
Sum[i] = readint() + Sum[i-1];
}
inline int64 GetY(int64 i) {
return opt[i] + i*i + (2*L+2) * (i + Sum[i])
+ Sum[i] * Sum[i] + 2 * i * Sum[i];
}
inline int64 GetX(int64 i) { return i + Sum[i]; }
inline int64 pow2(int64 x) { return x * x; }
int Hd, Tl, Q[(MAXN+10)<<1];
void Work() {
Hd = 1, Tl = 0;
opt[0] = 0; Q[++Tl] = 0;
for(int i = 1; i <= N; i++) {
while(Tl - Hd + 1 >= 2 &&
(GetY(Q[Hd+1]) - GetY(Q[Hd])) <= (GetX(Q[Hd+1]) - GetX(Q[Hd])) * 2 * (i + Sum[i]))
++Hd;
int j = Q[Hd];
opt[i] = opt[j] + pow2( (i - (j+1) + Sum[i] - Sum[j]) - L );
while(Tl - Hd + 1 >= 2 &&
(GetY(Q[Tl]) - GetY(Q[Tl-1])) * (GetX(i) - GetX(Q[Tl]))
>= (GetX(Q[Tl]) - GetX(Q[Tl-1])) * (GetY(i) - GetY(Q[Tl])))
--Tl;
Q[++Tl] = i;
}
printf("%lld", opt[N]);
}
int main() {
Init(); Work();
return 0;
}
BZOJ3675
题意
小H最近迷上了一个分隔序列的游戏。在这个游戏里,小H需要将一个长度为n的非负整数序列分割成k+1个非空的子序列。为了得到k+1个子序列,小H需要重复k次以下的步骤: 1.小H首先选择一个长度超过1的序列(一开始小H只有一个长度为n的序列——也就是一开始得到的整个序列); 2.选择一个位置,并通过这个位置将这个序列分割成连续的两个非空的新序列。 每次进行上述步骤之后,小H将会得到一定的分数。这个分数为两个新序列中元素和的乘积。小H希望选择一种最佳的分割方式,使得k轮之后,小H的总得分最大。 $2 \le n \le 100000,1 \le k \le \min(n -1,200)$ .
思路
我们知道暴力DP是 $O(n^3k)$ 的复杂度,只有 22pts 。
状态转移方程里面必须有 $k$ ,所以要想办法把区间 DP 转为序列 DP 来降低复杂度。注意到划分的顺序对于答案没有影响,我们可以考虑对于每个块计算贡献。不妨设序列为 $\{c_n\}$ , 如果 $\sum_{1 \le i \le k} c_i = \sumc(k)$ ,那么每个块 $[p, q]$ 的贡献是 $\sumc(p-1) \cdot [\sumc(q)-\sumc(p-1)]$ (想一想,为什么只计算左侧贡献).
这样就可以有一个 $O(n^2k)$ 的做法:如果 $f(i, p)$ 为划分好 $[1, i]$ 之后且还剩下 $p$ 次划分的答案,那么就有 $f(i,p)=\max\{f(j,p+1)+ \sumc(j) \cdot [\sumc(i) - \sumc(j)] \vert 0 \le j \le i-1\}$ .
这个式子是二维的,不过每次递推都只用了第二维上一层的信息,所以和一维的情况类似,同样可以应用斜率优化。不过从最小值变成了最大值,所以式子的形式上面稍有变化。凸壳也变成了上凸的。
对于每个确定的 $p$ ,只会用到 $f(i, p+1)$ 的信息。我们不妨记 $f(i, p+1) = g(i)$ ,就变成了斜率优化的形式。
我们设 $\alpha > \beta$ 且取 $j=\alpha$ 优于 $j=\beta$ ,则有
\[g(\alpha) + \sumc(\alpha) \cdot [\sumc(i) - \sumc(\alpha)] > g(\beta) + \sumc(\beta) \cdot [\sumc(i) - \sumc(\beta)]\]化简后为
\[[g(\alpha) - \sumc^2(\alpha)] - [g(\beta) - \sumc^2(\beta)] > \sumc(i)\cdot[\sumc(\beta) - \sumc(\alpha)]\]设 $y_j = g(j) - \sumc^2(j), x_j = \sumc(j)$ ,于是
\[\frac{y_{\alpha} - y_{\beta}}{x_{\alpha} - x_{\beta}} > -\sumc(i)\]显然 $x_j$ 单调递增。类似于第一个例题,我们可以证明,如果 $K(\alpha, \beta) = \frac{y_{\alpha} - y_{\beta}}{x_{\alpha} - x_{\beta}}, \forall \alpha > \beta > \gamma$ ,若 $K(\alpha, \beta) \ge K(\beta, \gamma)$ ,最优解一定不在 $j = \beta$ 取得。于是图形一定是上凸的。注意到 $-\sumc(i)$ 单调递减,所以用单调队列处理的时候,类似上题,直接弹出队首即可。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long int64;
const int MAXN = 1e5, MAXK = 200;
int64 N, K, Sum[MAXN+10], opt[MAXN+10][2]; int to[MAXN+10][MAXK+10];
int Hd = 1, Tl = 0, Q[MAXN+10];
inline int readint() {
int f=1, r=0; char c=getchar();
while(!isdigit(c)) { if(c=='-')f=-1; c=getchar(); }
while(isdigit(c)) { r=r*10+c-'0'; c=getchar(); }
return f*r;
}
#define GetY(i, p) (opt[(i)][((p)+1)&1] - Sum[(i)] * Sum[(i)])
#define GetX(i) (Sum[(i)])
int main() {
int64 Ans = 0, MaxP = 0;
static int S[(MAXN+10)<<1]; // std::stack<int> 非常慢!!!!!!!
N = readint(); K = readint();
for(int i = 1; i <= N; i++)
Sum[i] = readint() + Sum[i-1];
{
memset(opt, 0xdf, sizeof(opt));
opt[0][K&1] = 0;
for(int p = K-1; p >= 0; p--) {
Hd = 1, Tl = 0; Q[++Tl] = 0;
for(int i = 0; i <= N; i++) opt[i][p&1] = 0xdfdfdfdfdfdfdfdfLL;
for(int i = 1; i <= N; i++) {
while(Tl - Hd + 1 >= 2 &&
(GetY(Q[Hd+1], p) - GetY(Q[Hd], p)) >= (-Sum[i]) * (GetX(Q[Hd+1]) - GetX(Q[Hd])))
++Hd;
int j = Q[Hd];
opt[i][p&1] = opt[j][(p+1)&1] + (Sum[i] - Sum[j]) * Sum[j];
to[i][p] = j;
while(Tl - Hd + 1 >= 2 &&
(GetY(i, p) - GetY(Q[Tl], p)) * (GetX(Q[Tl]) - GetX(Q[Tl-1]))
>= (GetX(i) - GetX(Q[Tl])) * (GetY(Q[Tl], p) - GetY(Q[Tl-1], p)))
--Tl;
Q[++Tl] = i;
}
}
for(int i = 1; i <= N-1; i++)
if(opt[i][0&1] + Sum[i] * (Sum[N] - Sum[i]) >= Ans) {
Ans = opt[i][0&1] + Sum[i] * (Sum[N] - Sum[i]);
MaxP = i;
}
printf("%lld\n", Ans);
for(int i = MaxP, j = 0; j <= K; i = to[i][j], j++)
S[++S[0]] = i;
--S[0];
while(S[0]) {
int64 t = S[S[0]]; --S[0];
printf("%lld ", t);
}
}
return 0;
}
四边形不等式
挖坑待填