填坑ing…
概述
数论是研究整数的学问。初等数论的基础主要包括同余,扩展欧几里得定理,费马小定理,欧拉定理等。
同余
基本性质
同加 \(\large a \equiv b \pmod m \Leftrightarrow a+c \equiv b+c \pmod m\)
同减 \(\large a \equiv b\pmod m \Leftrightarrow a-c \equiv b-c \pmod m\)
同乘 \(\large a \equiv b\pmod m \Leftrightarrow a \cdot c \equiv b \cdot c \pmod m\)
同乘逆元 \(\large a \equiv b \pmod m \Leftrightarrow a \cdot c^{-1} \equiv b \cdot c^{-1} \pmod m\)
扩展欧几里得定理
作用
求解如下的丢番图方程之整解:
\[ax+by=c\]裴蜀定理
上述方程有整数解,当且仅当$(a,b)|c$。
原因很显然:既然 $ax+by=(a,b)$ 恒定有解,上述方程要有解,就得是两边同时乘上一个整数。
有了上述定理,对任意方程 $ax+by=c$ 的求解,就转为了对于 $ax+by=(a,b)$ 的求解。
如何对 $ax+by=(a,b)$ 求解呢?
扩展欧几里得定理
\(large ax+by=(a,b) \Rightarrow bx'+(a \text{ mod } b)y'=(b,a \text{ mod } b\)
由欧几里得定理: \(large (a,b)=(b,a \text{ mod } b\)
于是 \(large ax+by = bx'+(a \text{ mod } b) \cdot y'=bx'+(a-\lfloor \frac{a}{b} \rfloor \cdot b) \cdot y\)
即 \(large ax+by=ay'+b\cdot(x'-\lfloor \frac{a}{b} \rfloor \cdot y'\)
显然有
\[\large \begin{cases} x=y'\\ y=x'-\lfloor \frac{a}{b} \rfloor \cdot y' \end{cases}\]于是扩展欧几里得定理得证。
多解
如果上述方程有解,则有无穷组解。初始解 $(x_0,y_0)$ 保证 $|x_0|+|y_0|$ 最小。 而且有: \(\large \begin{cases} x=x\_0-t \cdot \frac{b}{(a,b)}\\ y \,=y\_0+t \cdot \frac{a}{(a,b)} \end{cases}\) 其中$ t \in \mathbb{Z}$。
解同余方程
To Be Done
代码
注意,即使a和b属于int,x和y也可能爆int!
void exgcd(int a, int b, int &d, int &x, int &y) {
if(b==0) { d=a, x=1, y=0; }
else {
exgcd(b, a%b, d, y, x); y-=x*(a/b);
}
}
例题
洛谷P1516-青蛙的约会 To Be Done
逆元
由同余定义显然有: \(large ax \equiv c \; \pmod b \Leftrightarrow ax+by=c\)
于是 \(\large a \cdot a^{-1} \equiv 1 \pmod b\Leftrightarrow a \cdot a^{-1} +by=1\)
有解的充要条件是 \(\large (a,b)|c\)
而$c=1$,于是 \(\large (a,b)=1\)
综上,$a$ 存在模 $b$ 意义下的乘法逆元的充要条件是$(a,b)=1$,即 $a,b$ 互质。 当逆元存在时,显然可以由扩展欧几里得定理得出一组解。注意通过上面提到的多解的判断把 $x$ 变为尽可能小的正数。这样求出的一定是最小的逆元。
应用费马小定理
显然,由于$a^{p-1} \equiv 1 \pmod p$,可知$a \cdot a^{p-2} \equiv 1 \pmod p$。于是$a^{p-2}$就是$a$在模$p$意义下的一个逆元。要求$p \in \mathbb{P}$且$p \nmid a$。用快速幂求出即可。
应用欧拉定理
同上。求$a^{\varphi(m)-1}$即可。
费马小定理
\(\large \forall a \in \mathbb{Z}, p \in \mathbb{P},p \nmid a,\;\;a^{p-1} \equiv 1 \pmod p\)
证明: \(\large \binom{p}{m}=\frac{p!}{m!(p-m)!}\)
当$p \in \mathbb{P}, m \neq 1且m \neq p$时,分子的$p$不可能被分母约去。
因此$p | \tbinom{p}{m}$。
又由二项式定理:
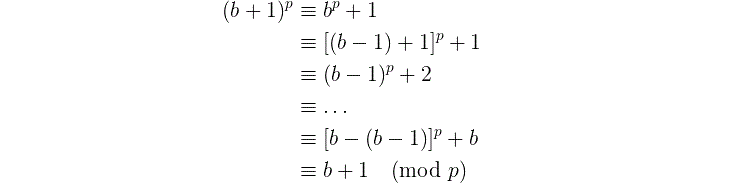 令$a=b-1$,则
\(a^p \equiv a \pmod p\)
令$a=b-1$,则
\(a^p \equiv a \pmod p\)
即 \(a^{p-1} \equiv 1 \pmod p\)
得证。
例题
To Be Done
底和顶
定义: \(n = \lfloor x \rfloor \Leftrightarrow n \le x < n+1 \\ n = \lceil x \rceil \Leftrightarrow n-1 < x \le n\) 常用不等式: \(x < n \Leftrightarrow \lfloor x \rfloor < n \\ n < x \Leftrightarrow n < \lceil x \rceil \\ x \le n \Leftrightarrow \lceil x \rceil \le n \\ n \le x \Leftrightarrow n \le \lfloor x \rfloor\) 常记为”左实底,右实顶,若取等,则相反”.