定义
概念
有效子矩形:内部不含有任何障碍点的矩形。
极大有效子矩形:一个有效子矩形,如果不存在一个比它更大而且包含它的有效子矩形,就称它为极大有效子矩形。
最大有效子矩形:整个矩形中面积最大的有效子矩形。
约定使用$S$表示障碍点的数量,整个矩形的大小为$N \times M$。
定理1:极大化思想
所有的极大有效子矩形中,一定包含着最大有效子矩形。
证明: 如果一个最大有效子矩形不是一个极大子矩形,那么就一定存在一个比它更大而且包含它的有效子矩形,这就与它是最大有效子矩形相矛盾。故原命题得证。
定理2:极大子矩形性质
极大子矩形的边界一定不能再扩展,即:要么边界上面有障碍点,要么边界与整个矩形的边界重合。
算法1
利用上述思想,我们可以设计一种复杂度为 $O(S^2)$ 的求解最大子矩形的算法。下列叙述中,障碍点都分布在坐标系的整点上。
首先把极大子矩形分为4种情况:
- 左右边界都与矩形左右边界重合
- 左边界与矩形边界不重合,右边界与矩形边界重合
- 左右边界都不与矩形边界重合。
- 左边界与矩形边界重合,右边界与矩形边界不重合
针对四种情况逐一讨论如下:
情况1
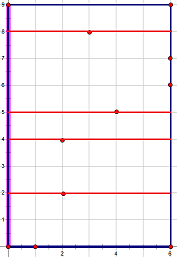
在预处理时解决:如下图,把点按照纵坐标排序,再将每格分别计算即可。注意障碍点在边界,挡不住任何矩形的情况。
情况2、情况3
把点按照横坐标升序排序。首先枚举左边界点。对于某个确定的左边界,依次枚举它右边的所有点(注意跳过与它坐标相同的点)。同时维护当前的极大子矩形的上下边界。在遇到右边任何一个点之前,上下边界的值为$M$和$0$。每次遇到一个点,就判断其纵坐标是否在上下边界内,如果不是就跳过,否则以这个点为右边界,当前的上下边界为极大子矩形上下边界,计算这个极大子矩形的面积。
接着用这个点更新上下边界:如果它的纵坐标小于左边界点就更新下边界,如果它的纵坐标大于左边界点就更新上边界,而如果二者相等就可以停止搜索(接着搜索没有意义,因为找到的不是极大子矩形)。
情况4
把点按照横坐标降序排序,再从右往左进行上述过程即可。
实现
最大子矩形模板题
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
const int MAXS = 5000;
struct Point{
int x,y;
Point(){}
Point(int x_,int y_):x(x_),y(y_){}
}P[MAXS+10];
int N,M,sz,Ans;
bool cmp1(Point a,Point b){ return a.y<b.y; }
bool cmp2(Point a,Point b){ return a.x<b.x; }
bool cmp3(Point a,Point b){ return a.x>b.x; }
inline int readint(){
int f=1,r=0;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){r=r*10+c-'0';c=getchar();}
return f*r;
}
int main(){
N=readint();M=readint();
sz=readint();
for(int i=1;i<=sz;i++) {
P[i].x=readint();
P[i].y=readint();
}
P[++sz]=Point(0,0);P[++sz]=Point(N,0);
P[++sz]=Point(N,M);P[++sz]=Point(0,M);
sort(P+1,P+sz+1,cmp1);
for(int i=1;i<=sz-1;i++)
for(int j=i+1;j<=sz;j++)
if(P[j].y!=P[i].y) {
Ans=max(Ans,(P[j].y-P[i].y)*N);
if(P[j].x!=0 && P[j].x!=N) break;
}
sort(P+1,P+sz+1,cmp2);
for(int i=1;i<=sz-1;i++){
int up=M,down=0;
for(int j=i+1;j<=sz;j++)
if((P[i].x!=P[j].x && down<P[j].y && P[j].y<up) || P[j].x==N) {
Ans=max(Ans,(P[j].x-P[i].x)*(up-down));
if(P[i].y==P[j].y) break;
if(P[j].y>P[i].y)
up=min(up,P[j].y);
else
down=max(down,P[j].y);
}
}
sort(P+1,P+sz+1,cmp3);
for(int i=1;i<=sz-1;i++){
int up=M,down=0;
for(int j=i+1;j<=sz;j++)
if((P[i].x!=P[j].x && down<P[j].y && P[j].y<up) || P[j].x==0) {
Ans=max(Ans,(P[j].x-P[i].x)*(up-down));
if(P[i].y==P[j].y) break;
if(P[j].y>P[i].y)
up=min(up,P[j].y);
else
down=max(down,P[j].y);
}
}
printf("%d",Ans);
}
算法2
同样利用极大化思想,我们可以设计出一种复杂度与障碍点个数无关的算法。此时障碍点分布在格子内部。
补充定义
便于叙述,定义如下概念:
有效竖线:除了两个端点之外没有覆盖任何障碍点的竖线。(两个端点可以覆盖障碍点,也可以不覆盖)
悬线:上端点覆盖了障碍点,或是与整个矩形的上边缘重合的有效竖线。
悬线对应的矩形:把一条悬线向左右尽量移动,所得到的有效子矩形称为悬线对应的矩形。
定理3
所有悬线对应的矩形中一定包含最大子矩形。
方法1
显然,可以在$O(NM)$的时间复杂度之内计算出以每个点为下端点的悬线。
悬线长可以递推得知:$h(x,y)=\begin{cases} h(x-1,y)+1 & \text{ if } W(x,y)=0 \ 0 & \text{ if } W(x,y)=1 \end{cases}$
对于某一行的某一条悬线,可以在它左右分别找出同一行中离它最近的、比它短的悬线。显然,找出的悬线所夹的宽度乘上当前悬线长度,即为这个悬线对应的矩形的面积。(如果不存在这样的悬线,则认为此悬线横坐标为$0$/$M+1$)
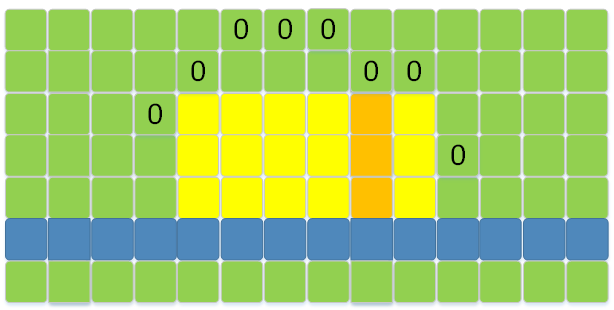
如下图中O为障碍点,蓝色行的上一行为当前行,橙色部分为当前悬线,橙色和黄色部分为当前悬线对应的矩形。
试着优化找出同一行中离它最近的、比它短的悬线的操作:利用单调栈的单调性即可。
方法2
也可以利用递推求解:
令$lc(x,y),rc(x,y)$为点$(x,y)$与左右的第一个障碍点之间的距离(边界也看作障碍点)
则有:
$\begin{cases} lc(x,y)=\begin{cases} lc(x,y-1)+1 & \text{ 若 } W(x,y)=0 \ 0 & \text{ 若 } W(x,y)=1 \end{cases}\ rc(x,y)=\begin{cases} rc(x,y+1)+1 & \text{ 若 } W(x,y)=0 \ 0 & \text{ 若 } W(x,y)=1 \end{cases} \end{cases}$
有了障碍点距离的递推式,就可以递推求出一条悬线向左/向右最多能移动的距离。
令$l(x,y),r(x,y)$为这个距离,则有:
$\begin{cases} l(x,y)=\min\begin{cases} l(x-1,y) & \text{ 若 } x>1 \text{ 且 } W(x-1,y)=0\ lc(x,y) \end{cases}\ r(x,y)=\min\begin{cases} r(x-1,y) & \text{ 若 } x>1 \text{ 且 } W(x-1,y)=0\ rc(x,y) \end{cases} \end{cases}$
然后即可求出悬线对应的矩形的面积。
实现
例题:CodeVS-2491-玉蟾宫
悬线法模板题
#include <cstdio>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
const int MAXN = 1000;
int N,M,Ans,W[MAXN+10][MAXN+10],h[MAXN+10][MAXN+10],
l[MAXN+10][MAXN+10],r[MAXN+10][MAXN+10],lc[MAXN+10][MAXN+10],rc[MAXN+10][MAXN+10];
inline char readc(){
int c=getchar();
while(c^EOF && c^'R' && c^'F') c=getchar();
return c;
}
inline int readint(){
int f=1,r=0;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1; c=getchar();}
while(isdigit(c)){r=r*10+c-'0'; c=getchar();}
return f*r;
}
int main(){
N=readint();M=readint();
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)
W[i][j]=(bool)(readc()=='R');
for(int i=1;i<=N;i++) {
for(int j=1;j<=M;j++)
lc[i][j]=(W[i][j]?0:lc[i][j-1]+1);
for(int j=M;j>=1;j--)
rc[i][j]=(W[i][j]?0:rc[i][j+1]+1);
}
memset(l,0x3f,sizeof(l));
memset(r,0x3f,sizeof(r));
for(int i=1;i<=N;i++)
for(int j=1;j<=M;j++)
h[i][j]=(W[i][j]?0:h[i-1][j]+1);
for(int i=1;i<=N;i++) {
for(int j=1;j<=M;j++)
if(!W[i][j]){
l[i][j]=min(l[i-1][j],lc[i][j]);
r[i][j]=min(r[i-1][j],rc[i][j]);
Ans=max(Ans,(l[i][j]+r[i][j]-1)*h[i][j]);
}
}
printf("%d",3*Ans);
}