自己对最近网络流学习的一些整理和理解……
如果有什么错误,请立即纠正,非常感谢。
这边Blog的排版估计很渣……我懒得管了,丢个 $\LaTeX$ 版的吧……戳我
UPD:发现洛谷上面的网络流题目严重不全……这么多年省选也不会只考了10道网络流啊……翻了翻hzwer的博客,屯了40几题,准备先用一个星期做个二十几道,剩下的边练DP边带着做
我已经做了 8 题
✅bzoj4205 bzoj3308 ✅bzoj1283 ✅bzoj3894 bzoj1797 bzoj3996 ✅bzoj3876 ✅bzoj2756 bzoj2718 ✅bzoj2007 ✅bzoj2893 bzoj3158 ✅bzoj1822 ✅bzoj2929 ✅bzoj1520 bzoj2324 bzoj1324 bzoj3698 bzoj2561 bzoj3396 bzoj3504 bzoj2502 bzoj2055 bzoj1532 bzoj1930 bzoj2661 bzoj1711 bzoj1458 bzoj3280 bzoj3275 bzoj2768 bzoj2245 bzoj1391 bzoj2127 bzoj2132 bzoj3171 bzoj1934 bzoj2424 bzoj1305 bzoj1189 bzoj1066 bzoj1191 bzoj3693 cf498c vijos1891 poj2396 zoj3229 codevs1222 雅礼集训day2t2
最大流
二分图相关
定义与算法
概念
没有奇环的图是二分图。二分图可以分成2个部分,每个部分内没有边。为了方便可以称为左点和右点。
匹配:一组顶点不相交的边集合
完美匹配:每个点都是匹配点的匹配
未盖点:不与任何匹配边邻接的点
交替路: 未匹配边-匹配边-未匹配边-匹配边-未匹配边……
增广路:以未匹配边结尾的交替路
增广路定理:对于任意图,图上匹配为最大匹配的充要条件是没有增广路
KM算法
求二分图最大权完美匹配 。
给每个节点分配一个顶标。定义满足 $L_i+L_j \geq w_{i, j}$ 的顶标 $L$ 是可行顶标,满足 $L_i+L_j = w_{i, j}$ 的边及其顶点构成了相等子图。我们可以证明,相等子图有完美匹配,则它是原图的最大匹配。证明过程对所有的“最大”/“最小”问题都很有启发性:先证明上界,再碰到上界。由于可行顶标的性质,显然相等子图匹配权值 $\geq$ 原图任何一个完美匹配。在相等子图中可行顶标式子的“=”取得,于是这是原图的最大权匹配。得证。
KM算法步步都用到了贪心的思想。首先贪心地构造出初始相等子图,不妨令每个左点顶标为出边边权最大值,右点顶标为0。每次先从左点开始进行匈牙利算法,求相等子图的一个匹配。如果这个匹配是完美匹配,那么算法结束,否则我们需要让更多边加入进来,从这个点完成一次增广,再从下一个点开始进行匹配。我们给每个在匈牙利算法中访问了的左点顶标减去一个数 $d$ ,给访问了的右点顶标加上一个数 $d$ ,来加入一条边。
分析可知,如果设左点中访问了的点为 $\mathbb{X}$ 集,未访问的为 $\mathbb{X’}$ 集,右点相应为 $\mathbb{Y, Y’}$ 集,那么,$\mathbb{X} \rightarrow \mathbb{Y’}$ 一定没有边(否则匈牙利树可以继续生长), $\mathbb{X’} \rightarrow \mathbb{Y}$ 的边一定是未匹配边;$\mathbb{X’} \rightarrow \mathbb{Y’}$ 也一样,不过它和我们这步操作无关。再来分析刚才的 $d$ 应该设为多少。显然 $d$ 应该贪心地取 $ \min{L_u + L_v - w_{u, v} \mid u \in \mathbb{X}, v \in \mathbb{Y’}} $ 。只能取这个值,因为如果 $d$ 更大,对于取得 $\min$ 的边来说,$u$ 一端顶标就不再可行;如果 $d$ 更小,那么就没有新边加入。
加了这条边之后原图有什么变化?对于两端都是已访问节点的边而言,由于两端顶标和不变($(L_u - d) + (L_v + d) = L_u + L_v$),它是否在相等子图这点并不会改变。对两端都不是已访问节点的边也是一样。左端在 $\mathbb{X}$ 右端在 $\mathbb{Y’}$ 的边中边权最大的会加入相等子图。而左端在 $\mathbb{X’}$ 右端在 $ \mathbb{Y}$ 的边,虽然可能离开相等子图,但是它们本来就不是匹配边,离开了也没有关系。不断进行这步操作直到可以增广。于是这步操作至少引入了一条匹配边。由于上述贪心,最终求出的一定是最大完美匹配。
注意,这个算法只适用于有完美匹配的情况。没有完美匹配的情况下,如果要求最大权匹配,就得用费用流了。
常用性质:
-
$L_u + L_v \geq w_{u,v}$
- 最大权匹配等于最小顶标和
- 算法结束的时候 $\sum L_i$ 最小
König定理
无权二分图的最大基数匹配等于最小点覆盖。
从网络流的角度容易证明。选择某点到点覆盖集合中,则割它与 s/t 相连的边。求最大匹配,可以用最大流。由最大流最小割定理,它们是等价的。
应用与建模
以下的应用,均是在二分图中的。
最小点覆盖
定义:选出最少的点,覆盖图中所有边。
不带权的时候,由König定理易得。求最大基数匹配即可。
带权的时候,考虑用不带权的类比。不带权的时候,我们是把最大基数匹配(最大流)转为了最小点覆盖(最小割)。现在点有点权,我们同样考虑用最小割建模。建立超级源点 s ,汇点 t ,s 向左点连容量为点权的边,右点向 t 连容量为点权的边,原二分图中边的容量为无穷大。显然割一定只和 s, t 有关,割那条边就代表把对应点选入最小点覆盖模型1。
最大点独立集
定义:选出最多的点,使得任意边两端点最多有一个被选中。
这个问题和最小点覆盖互补。先考虑不带权情况。我们把图上的点划分成2个集合。最小点覆盖集关于所有顶点的补集,即为最大点独立集。为什么呢?我们考虑图中每条边。其顶点至少一个属于最小点覆盖集,取补集后,最多一个属于最大点独立集,符合其定义。而最小点覆盖集是最小化集合中点数目,取补集后为最大化点独立集中点数目,与最大点独立集的优化目标一致。带点权的情况的证明是类似的。
所以说,要求最大点独立集大小,用总点数/总点权减去最小点覆盖的大小即可。
DAG的最小路径覆盖 / 有向图的最小圈覆盖
定义:前者为在DAG上选择最少条点不相交的路径,使得这些路径上含有图上所有点。
后者为在有向图最少个点不相交的环,使得环上有图上所有点。(注意可以有自环,而且有些时候自环必不可少)
先看最小路径覆盖。同样分为不带权和带权两种情况。我们把每个点拆成 2 个,一个为左点,一个为右点。考虑在最小路径覆盖中,除了路径结尾每个点都有唯一的后继,也就是说每个点和它的后继点一一匹配。从另一个角度看,每次匹配后继点,对应于把两条路径合并起来,并的次数最多的时候,最终剩下的路径条数也就最少了2。要是每个边有代价,并且要求最小化总代价和呢?给匹配边赋边权。在路径之间转移有代价?考虑从 s 直接连边,也就是表示某个点是 s 这个虚拟点的后继节点。(SDOI2010星际竞速)
后者和前者相似,也是“匹配后继”的思想。不过有解的充要条件是对应二分图有完美匹配。(可以用置换来思考:有完美匹配,即可以看作一个置换,而置换一定可以分解为若干循环乘积)
稳定婚姻问题
用图论的话来说,把边权变成了“双向不同”的。 $u \rightarrow v$ 边权大,$ v \rightarrow u$ 边权不一定大。求一个匹配使得不存在 $<u,v> \in \mathbb{E}$ ,其中 $u$ 已经和 $b$ 匹配,而 $v$ 已经和 $a$ 匹配,且对于 $u$ 来说 $b$ 不如 $v$ , 而且对于 $v$ 来说 $a$ 不如 $u$ 。
Gales-Shapley 算法:每次男子按照喜爱度大到小依次求婚,女子如果发现当前配偶对自己吸引力不如现在求婚的大,就可以抛开当前配偶与现在求婚的结婚。可以证明最后的解一定稳定。
建模套路
- 给出矩阵,看作邻接矩阵,转为二分图来理解 (uvaoj11419、ZJOI矩阵游戏)
- 给出矩阵,黑白染色,再把两种颜色的看成二分图(骑士共存问题、清华集训2017无限之环)
- 与“阶段”有关的匹配问题,按照阶段拆点建图。有时候阶段对应点很多,要动态开(SCOI修车,NOI美食节)
- 二分图完美匹配等价于置换,利用置换循环的关系帮助思考(ZJOI矩阵游戏)
最小割
最小割:一个 s-t 划分
最大流最小割定理:s-t 最大流 = s-t 最小割
满流边不一定都在最小割中。跑完Dinic后在残量网络中DFS/BFS求出最小割。(考虑Amber神犇论文里面举的典型错误!)
建模
-
涉及到集合的划分问题,就想到最小割。(uvaoj1515,ZJOI狼和羊的故事)
- 有向图的最大闭合子图。
选 u, v 中的一个就会产生某个代价,但是都选不会造成更大影响。
- s 向每个非负权值点连边,每个负权值点向 t 连边,求出割 $[S,T]$ 后, $S-{s}$ 即最大闭合子图,其权值为 $\sum w_+ - c[S,T]$ 。
- 典型题目:
- NOI2009植物大战僵尸: 注意虽然没有自环,但是可能连环保护导致无敌,而且无敌点保护的点也无敌
- 文理分科:对称关系,不好下手?尝试找出“基准状态”,把对应的状态看成选/不选的关系。这样就把“选什么”的问题转为了“选不选”的问题。不妨假设最开始的时候全部选择文科。现在某些人改选理科,看能否增大收益。周围4个人+自己都选理科,可以获得某个收益。一般地,在多个条件都满足的情况下获得收益的模型,可以看成是一种“推导”,从而转化为最大权闭合子图。这里把每个人拆成3个点,代表相应决策:那个人自己选理科(获得理科收益,失去文科收益)、那个人和周围至少1个选理科(失去都选择文科的收益),那个人和周围都选理科(获得都选择理科的收益)。然后就可以容易地转化为最大权闭合子图求解。
- 寿司餐厅:“记忆性”等价于“选一个有代价,选多个代价不扩大”。直接用最大权闭合图即可。
- 无向图的最大密度子图。边和点都带有权值,求一个子图,最大化
- 显然是分数规划。首先二分答案 $x$ 。选了边,相邻点就要选,可以把每条无向边拆成 2 条有向边。再看最大闭合子图权值是否大于 0 ,从而调整二分的答案。(uvaoj Hard Life)(顺便吐槽下这个题目,卡精度,eps开1e-6 WA,开1e-8连样例都过不了,浪费了我 2 个多小时……)
- HNOI2013切糕:抓住“割使得 $s-t$ 不连通”的性质,要让某些边不能同时割,就是要在删除它们后图仍然连通
- NOI2010海拔:平面图最小割。想象割边从超级源点生长到超级汇点。原图中边逆时针转90度即为对偶图的边。
拆点拆边技巧
- 节点容量拆成边,转为边容量
- 某个东西有“阶段”的划分,每个阶段拆出一个点(固定分区内存管理、SCOI修车、NOI美食节)
- 二分图匹配是利用 s 到左点的容量来限制最多匹配 1 条边,可以类似地进行“三分图匹配”(酒店之王)
费用流
算法
SPFA-Edmonds-Karp / Primal-Dual
比较如下:(测试用题为洛谷费用流模板)
| Algorithm | Accepted | Time |
|---|---|---|
| Dijkstra+Pairing Heap+Primal Dual(O2) | Yes | 820ms |
| Dijkstra+std::priority_queue+Primal Dual(O2) | Yes | 832ms |
| Dijkstra+Binary Heap with decrease_key+Primal Dual(O2) | Yes | 888ms |
| Dijkstra+Pairing Heap+Primal Dual | Yes | 1236ms |
| Dijkstra+Binary Heap with decrease_key+Primal Dual | Yes | 1528ms |
| SPFA+Primal Dual(O2) | Yes | 1548ms |
| SPFA+Edmond Karp | Yes | 1596ms |
| SPFA+Primal Dual | Yes | 2184ms |
| Dijkstra+std::priority_queue+Primal Dual | No | 3036ms |
| SPFA+SLF+Primal Dual(O2) | No | 3204ms |
| SPFA+SLF+Primal Dual | No | 4740ms |
建模
求k条路径并最短路
- 求 $s \rightarrow t$ 的 $k$ 条路径,总长度最短。每条边容量 1 ,费用为边权,直接找固定流量的最小费用流。
最小费用可行流
-
最小费用循环流,也称最小费用可行流,对每个点都满足流量平衡的条件。消圈算法太慢,我们用建图技巧避开输入的负权边3。每个负权边 $<u, v>$ 拆成 $<ss, v>, <v, u>, <u, tt>$ 三条,容量均同原来的负权边,只有第二条边带上费用,费用为原来的费用的相反数。再找 $<ss, tt>$ 的最小费用流。最后把费用加上原图所有负权边权值和各自容量乘积即为答案。
- 为什么这么做?这就是“预先流满”的操作。既然 Bellman-Ford 算法无法处理负权环,我们就让图中的负权边预先流满,同时累加上流满它们的代价(显然为负数)。在流满之后,残量网络里面就没有负权边了。但是某些点,确切地说,那些与原来负权边相关的点就不再满足流量平衡的条件了。仔细分析发现,我们得给“预先流满”的流找个来头。我们不妨认为它们是从 $tt$ 流来的,一直流到 $ss$ 结束。这样的话,除了 $ss, tt$ , 其他点都满足了流量平衡的条件。$tt \rightarrow ss$ 流恰好流满了所有的负权边。既然我们已经把负权边流满了,我们再试图从 $tt$ 向 $ss$ 增广也没有意义了,因为以后的增广费用一定为正。所以我们令$<ss, v>, <u, tt>$ 的容量等于原来负权边的容量,费用为 0 。(其实就是流满后的反悔边!)
- 注意:这样求出的流在删掉附加边之后是不满足流量平衡条件的。如何满足?从 $ss$ 向 $tt$ 增广,以消去附加边!增广到与 $ss, tt$ 有关的边退出残量网络即可。这样就消掉了之前假定的 $tt \rightarrow ss$ 流,所有的流就都是来自图内部了,删掉 $ss, tt$ 以及与 $ss, tt$ 有关的边,图中就是最小费用可行流,对每个节点都满足流量平衡。 有人也许会问:在 $ss \rightarrow tt$ 增广的过程中,会引入负权环吗?这是不可能的。新图中边的费用均非负,如果要增广产生负权环,必定要沿着某个正环增广。而沿着正环增广不仅无益于增大 $s-t$ 流,还会徒增费用。也就是说,只要图中没有负环,增广后也不会有负环。所以这样一定可以求出合法的最小费用可行流。
残量网络如图。图上 边权为费用,容量均为1 。
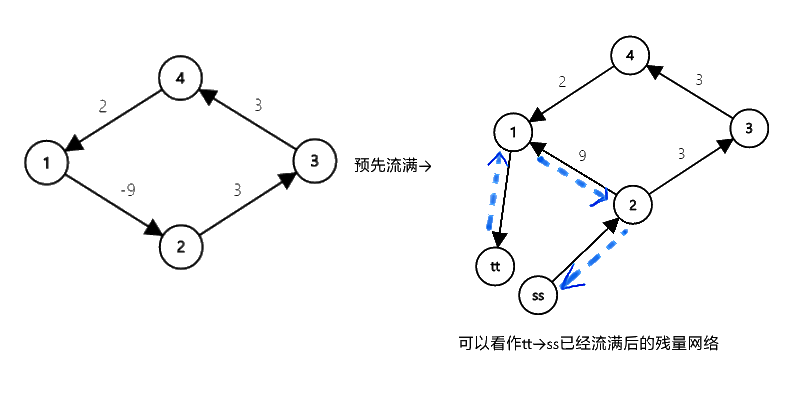
带负环的最小费用最大流
- 求 $s \rightarrow t$ 最小费用最大流。注意可以有负环,但是负环要有容量限制。先连上 $t \rightarrow s$ 的边,容量 $\infty$ ,费用 0 。用上面的方法求最小费用可行流。再从 s 往 t 增广(不拆 $t \rightarrow s$ 边,见上下界网络流)。两次增广的费用之和即为总的最小费用。
费用与流量成下凸函数的最小费用最大流
- 差分权值后拆边
- e.g. $cost = flow^2 \Rightarrow \begin{cases}cost=flow \ cost = 3\cdot flow \ cost = 5 \cdot flow \ \cdots\end{cases}$
注意事项
一般实际使用的时候,不直接建出与 ss, tt 有关的边,而是用一个数组记录到某个点的边总容量(费用相同,均为0),以去除重边。否则一堆重边,会TLE的很惨= =
上下界网络流
其思想与负权费用流建图有所不同。负权费用流建图的“预先流满”后尝试退流,而上下界网络流则是“强制流满”。
上下界可行流4
如下图,为一条下界为 $2$ ,上界为 $5$ 的弧。
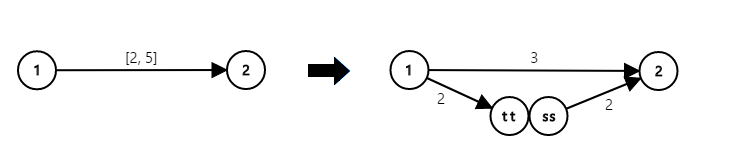 我们把下界非 0 的弧拆成必要弧和附加弧。必要弧一定要满流,附加弧不一定。
我们把下界非 0 的弧拆成必要弧和附加弧。必要弧一定要满流,附加弧不一定。
如何让必要弧满流?用附加源点。用 Dinic 找出从 ss 到 tt 的最大流,如果所有和 ss, tt 相关的边都满流,则求出了一个可行流。
上下界 $s-t$ 最大流
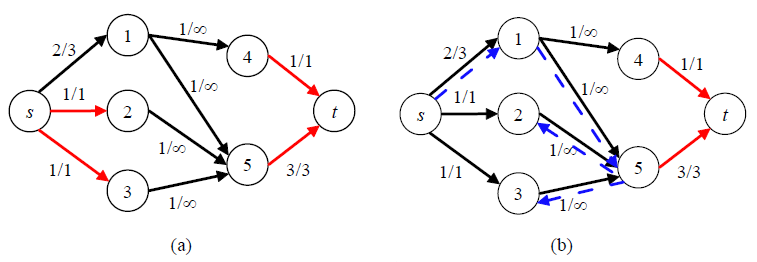
首先连接边 $<t, s>$ ,容量无穷大。然后找出一个上下界可行流,不拆 $<t, s>$ 边,直接求解 $s \rightarrow t$ 最大流即为答案。很多的资料都说要拆掉 $<t, s>$ 边,但仔细想想就会发现,这是不必要的。直接原封不动找 $s \rightarrow t$ 最大流就可以了。
下图为一个要求解上下界网络流的残量网络。
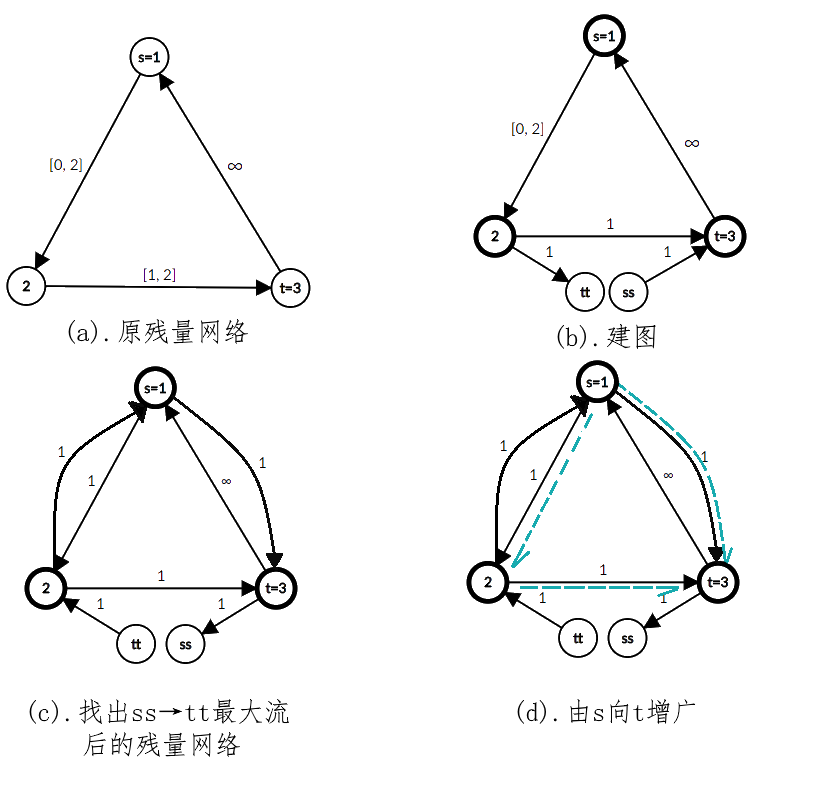 可以看出,最后一次增广刚好撤销了 $t \rightarrow s$ 边上的流量!于是最大流为2。
可以看出,最后一次增广刚好撤销了 $t \rightarrow s$ 边上的流量!于是最大流为2。
由于代表下界的必要弧已经拿出了原来的图,显然不可能增广到流量低于下界,所以一定合法。
上下界 $s - t$ 最小流
这个问题也只在有流量下界的时候有意义,因为流量下界为 0 时,最小流就是零流,没有什么可求的。
我们考虑流量的反对称性:
\[f(t, s) = -f(s, t)\] 也就是说 $t \rightarrow s$ 流量增加,等价于 $s \rightarrow t$ 流量减少。于是从 t 往 s 增广即可求出最小流。
有一点需要注意:求最小流的时候必须删掉最后加的 $<t,s>$ 弧及其反向弧。否则沿着新加的弧增广,最小流是无穷小。
最终答案为可行 $s-t$ 流减去增广的 $t-s$ 最大流。前者可以通过检查求完上下界可行流后 $<t,s>$ 边的流量得知。
答案可包含环流。
(好像还有一种更简单的方法5……但是没能理解……)
上下界最小费用可行流
同样是拆边法。但是不能允许必要弧退流。于是我们把必要弧和费用流的附加弧合并处理。对于非负费用边,我们把必要弧拉出来,建立弧 $<ss, v>, <u, tt>$ ,其容量均为下界,但是只有 $<ss,v>$ 带上与原弧相同的费用,从而避免必要弧重复计费。对于负费用边,见下图中(a), (b), (c)。 注意,在实际实现的时候,一定要合并重边!!!(AHOI支线剧情)方法是记录每个节点的盈余/亏欠流量,最后一起建与 $ss, tt$ 有关的边,并且预先记录流满所需费用。
这样求出的流是可以包含环流的。原因是我们建立了超级源汇点,把环拆开了。
上下界 $s-t$ 最小费用最大流
注意:可以有负环。大体思想就是把负权费用流和上下界费用流合二为一。(a) - (c) 步骤是连边 $<t,s>$ ,容量 $\infty$ ,费用0,把上下界最小费用最大流转为上下界最小费用可行流处理。(d) 步骤是在可行流基础上求最小费用最大流。注意:总的流量等于 (d) 步骤增广的流量,但是费用等于所有负权值的和+两次增广的费用。
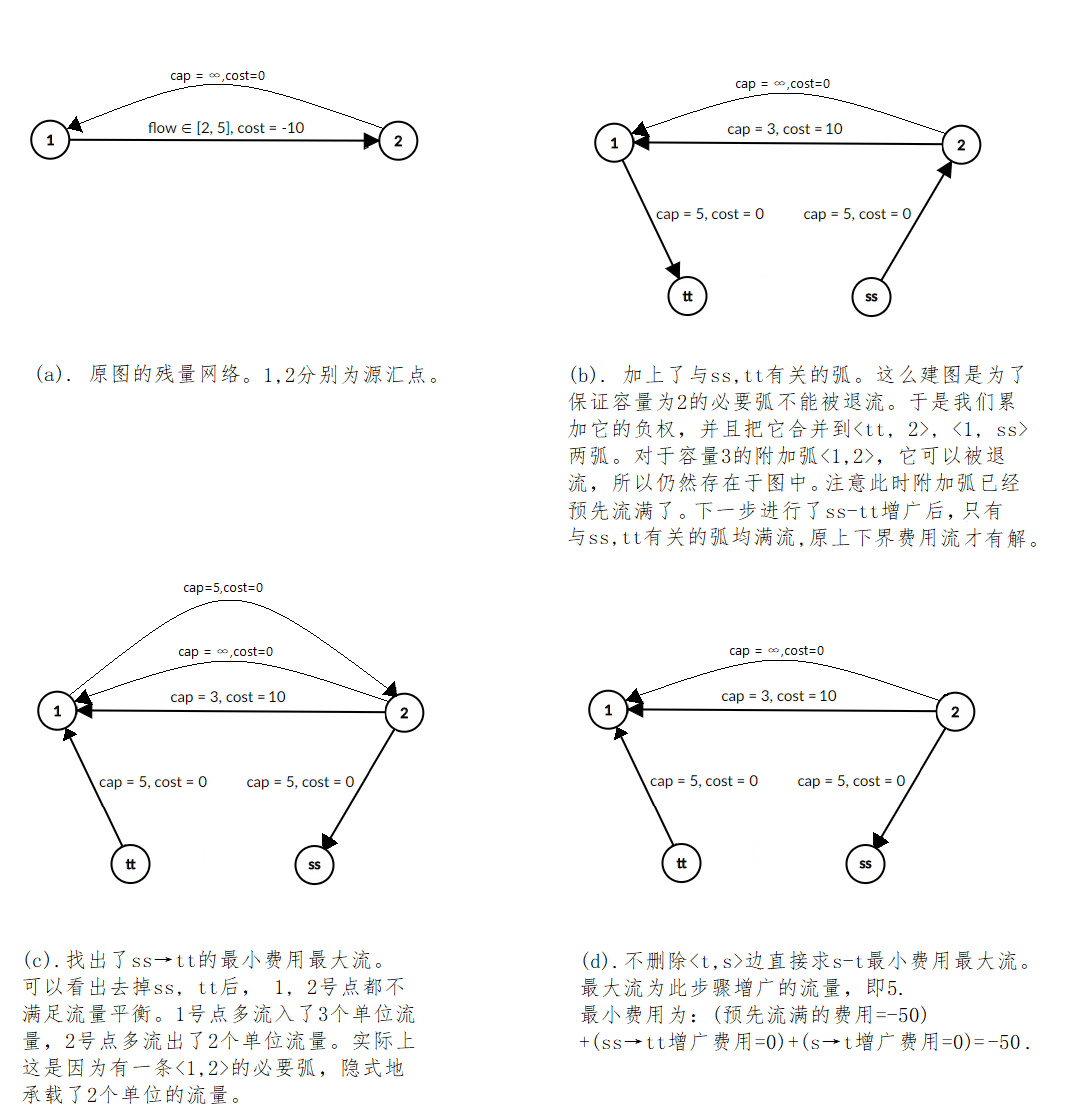
上下界 $s-t$ 最小费用流
同上下界 $s-t$ 最小费用最大流,不过要把求最小费用最大流改成求最小费用流,即在 $\underline{s-t}$ 距离非负时停止增广。
-
最小点覆盖和最小割的对应关系,感性理解是显然的。但是我并不会证明。如果有哪位神犇懂得证明请评论,我非常感谢。 当然,首先得有人看qwq ↩
-
参考了zkw神犇的Blog ↩
-
参考了liu_runda的Blog ↩